Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi giao điểm của AG với BC là E
Xét ΔABD có
G là trọng tâm
E là giao điểm của AG với BD
Do đó: E là trung điểm của BD và AG=2/3AE
Xét ΔAHD có \(\dfrac{AG}{AE}=\dfrac{AM}{AD}=\dfrac{2}{3}\)
nên GM//ED
=>GM//BD
mà BD\(\subset\left(BCD\right)\) và GM không thuộc mp(BCD)
nên GM//(BCD)
b: Gọi giao của AH với BC là F
Xét ΔABC có
H là trọng tâm
F là giao điểm của AH với BC
Do đó: F là trung điểm của BC và AH=2/3AF
Xét ΔAGE có \(\dfrac{AH}{AF}=\dfrac{AG}{AE}=\dfrac{2}{3}\)
nên HG//FE
mà \(FE\subset\left(BCD\right)\);HG không thuộc(BCD)
nên HG//(BCD)

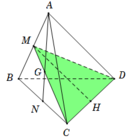
Gọi M; N lần lượt là trung điểm của AB và B C suy ra AN và MC cắt nhau tại G
Dễ thấy mặt phẳng (GCD) cắt đường thắng AB tại điểm M.
Suy ra tam giác MCD là thiết diện của mặt phẳng (GCD) và tứ diện.
Tam giác ABD đều, có M là trung điểm AB suy ra
Tam giác A BC đều, có

Chọn B.

Đáp án D
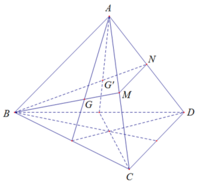
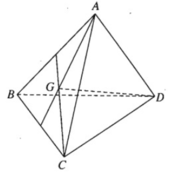
Trong(ABC), ta có: BG cắt AC tại M
Trong (ABD), ta có: BG’ cắt AD tại N
⇒ (BGG’) ∩ (ACD) = MN
Thiết diện cần tìm là (BMN)
Xét tam giác BMN có:
MN = 1 2 CD = a 2 ( MN là đường trung bình của tam giác ACD)
BM = BN = a 3 2 (BM, BN lần lượt là đường trung tuyến của tam giác ABC, ABD)
Áp dụng công thức heron:
S = p p - a p - b p - c = a 2 11 6

Gọi f là phép dời hình biến tam giác ABC thành tam giác A’B’C’.
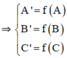
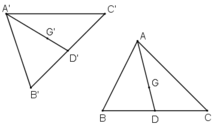
Gọi D là trung điểm của BC, D’ = f(D).
Gọi G là trọng tâm ΔABC, G’ = f(G).
+ B, D, C thẳng hàng ⇒ B’; D’; C’ thẳng hàng.
+ A; G; D thẳng hàng ⇒ A’; G’; D’ thẳng hàng.
+ B’D’ = BD = BC/2 = B’C’/2 ⇒ D’ là trung điểm B’C’.
+ A’G’ = AG = 2.AD/3 = 2.A’D’/3 ⇒ G’ là trọng tâm ΔA’B’C’.
Vậy phép dời hình f biến trọng tâm G của ΔABC thành trọng tâm G’ của ΔA’B’C’ (đpcm).


Gọi phép dời hình đó là f. Do f biến các đoạn thẳng AB, AC tương ứng thành các đoạn thẳng A'B', A'C' nên nó cũng biến các trung điểm M, N của các đoạn thẳng AB, AC tương ứng theo thứ tự thành các trung điểm M', N' của các đoạn thẳng A'B', A'C'. Vậy f biến các trung tuyến CM, BN của tam giác ABC tương ứng thành các trung tuyến C'M', B'N' của tam giác A'B'C'. Từ đó suy ra f biến trọng tâm G của tam giác ABC của CM và BN thành trọng tâm G' của tam giác A'B'C' là giao của C'M' và B'N'.

Gọi phép dời hình đó là f. Do f biến các đoạn thẳng AB, AC tương ứng thành các đoạn thẳng A'B', A'C' nên nó cũng biến các trung điểm M, N của các đoạn thẳng AB, AC tương ứng theo thứ tự thành các trung điểm M', N' của các đoạn thẳng A'B', A'C'. Vậy f biến các trung tuyến CM, BN của tam giác ABC tương ứng thành các trung tuyến C'M', B'N' của tam giác A'B'C'. Từ đó suy ra f biến trọng tâm G của tam giác ABC của CM và BN thành trọng tâm G' của tam giác A'B'C' là giao của C'M' và B'N'.

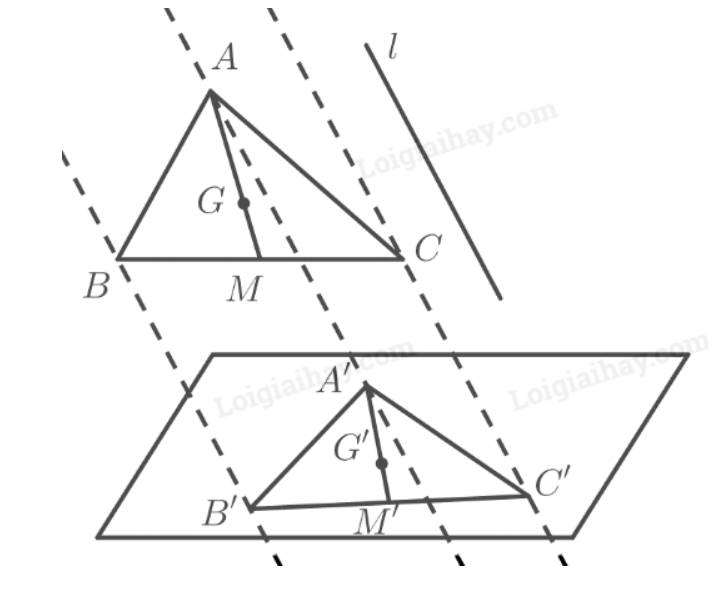
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(M\) nằm giữa \(B\) và \(C\) thì \(M'\) nằm giữa \(B'\) và \(C'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(MB = MC\) thì \(M'B' = M'C'\).
Vậy \(M'\) là trung điểm của \(B'C'\).
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(G\) nằm giữa \(A\) và \(M\) thì \(G'\) nằm giữa \(A'\) và \(M'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(AG = \frac{2}{3}AM\) thì \(A'G' = \frac{2}{3}A'M'\).
Vậy \(G'\) là trọng tâm tam giác \(A'B'C'\).
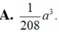
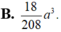
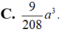
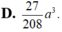
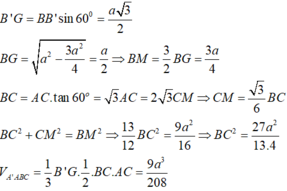

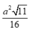
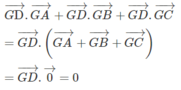
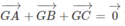 )
)
Kéo dài BG cắt AC tại N; CG cắt AB tại M
Có : SAGC = \(\frac{1}{2}\)h.GC ; SBGC = \(\frac{1}{2}\). k. GC mà SAGC = SGBC nên h = k
Mặt khác, SGAM = \(\frac{1}{2}\)h.GM ; SGBM = \(\frac{1}{2}\)k. GM
=> SGAM = SGBM
Lại có : tam giác GAM; GBM đều chung chiều cao hạ từ G xuống AB => đáy MA = MB => M là trung điểm của AB => CM là trung tuyến
+) Tương tự, từ SGAB = SGBC => N là trung điểm của AC => BN là trung tuyến
BN cắt CM tại G => G là trọng tâm tam giác ABC