Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

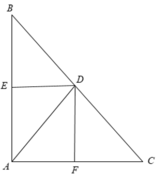
-Ta có: DE//AB, DF//AC (gt).
\(\Rightarrow\) AEDF là hình bình hành mà AD là tia phân giác của \(\widehat{BAC}\) (gt).
\(\Rightarrow\) AEDF là hình thoi.
-Xét △ABC có: DF//AC (gt).
\(\Rightarrow\dfrac{BF}{AB}=\dfrac{DF}{AC}\) (định lí Ta-let).
\(\Rightarrow1-\dfrac{DF}{AB}=\dfrac{DF}{AC}\)
\(\Rightarrow\dfrac{DF}{AB}+\dfrac{DF}{AC}=1\)
\(\Rightarrow DF.\left(\dfrac{1}{AB}+\dfrac{1}{AC}\right)=1\)
\(\Rightarrow DF.\left(\dfrac{1}{3}+\dfrac{1}{6}\right)=1\)
\(\Rightarrow DF.\dfrac{1}{2}=1\)
\(\Rightarrow DF=2\) (cm).
\(\Rightarrow P_{AEDF}=4.DF=4.2=8\left(cm\right)\) (do AEDF là hình thoi).

Lời giải:
$DF\parallel AE, DE\parallel AF$ nên $AEDF$ là hình bình hành
$P_{AEDF}=AE+DF+DE+AF$
Lại có:
$DF\parallel AC$ nên áp dụng định lý Talet:
$\frac{DF}{AC}=\frac{BF}{AB}$. Mà $AB=AC$ nên $DF=BF$
$DE\parallel AB$ nên áp dụng định lý Talet:
$\frac{CE}{AC}=\frac{DE}{AB}$ mà $AB=AC$ nên $CE=DE$
Do đó:
$P_{AEDF}=AE+BF+CE+AF=(AE+CE)+(BF+AF)=AC+AB=4+4=8$ (cm)

Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác
nên AEDF là hình vuông

Xét tứ giác AEDF có
DE//AF
AE//DF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
mà AD là tia phân giác
nên AEDF là hình vuông