Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha![]()
a.
Xét tam giác AMN và tam giác CGN có:
AN = NC (N là trung điểm của AC)
ANM = CNG (2 góc đối đỉnh)
MN = GN (gt)
=> Tam giác AMN = Tam giác CGN (c.g.c)
b.
MAN = GCN (tam giác AMN = tam giác CGN)
mà 2 góc nay ở vị trí so le trong
=> MB // CG
c.
MB // CG
=> BMC = GCM (2 góc so le trong)
AM = CG (tam giác AMN = tam giác CGN)
mà AM = MB (M là trung điểm của AB)
=> MB = CG
Xét tam giác MBC và tam giác CGM có:
MB = CG (chứng minh trên)
BMC = GCM (chứng minh trên)
MC là cạnh chung
=> Tam giác MBC = tam giác CGM (c.g.c)
MN = NG (gt)
=> N là trung điểm của MG
=> MN = NG = \(\frac{1}{2}MG\)
mà MG = CB (tam giác MBC = tam giác CGM)
=> MN = \(\frac{1}{2}BC\)
Chúc bạn học tốt![]()

tự kẻ hình nha
a) xét tam giác AMN và tam gáic CEN có
AN=NC(gt)
MN=NE(gt)
ANM=CNE( đối đỉnh)
=> tam giác AMN= tam giác CEN(cgc)
=> AM=CE(hai cạnh tương ứng) mà AM=MB=> MB=CE
=> CEN=AMN(hai góc tương ứng)
mà CEN so le trong với AMN mà A,M,B thẳng hàng=> MB//CE
c) từ MB//CE=> BMC=MCE( so le trong)
xét tam giác BMC và tam gíac ECM có
MC chung
BMC=MCE(cmt)
MB=CE(cmt)
=> tam gíac BMC= tam giác ECM(ccg)
d) từ tam giác BMC= tam giác CEM=> BCM=EMC( hai góc tương ứng), ME=BC( hai cạnh tương ứng)
mà BCM so le trong với EMC=> MN//BC
vì MN=NE mà ME=BC(cmt)
=> BC=2MN=> MN=1/2BC

a/ Xét \(\Delta ANM\)và \(\Delta CND\)có :
+) \(MN=ND\left(gt\right).\)
+) \(AN=NC.\)
+) Góc \(ANM\)= Góc \(NCD.\)
\(\Rightarrow\Delta ANM=\Delta CND\left(c.g.c\right).\)
\(\Rightarrow CD=AM.\)
Mà \(AM=BM.\)
\(\Rightarrow CD=BM.\)
b/ Xét \(\Delta ABC\)có \(M,N\)lần lượt là trung điểm của \(AB,AC.\)
\(\Rightarrow MN\)là đường trung bình của \(\Delta ABC.\)
\(\Rightarrow MN//BC\)và \(MN=\frac{1}{2}BC.\)
c/ Ta có \(MN=\frac{1}{2}BC.\)
\(\Rightarrow2MN=BC.\)
\(\Leftrightarrow MD=BC.\)
Xét tứ giác \(BMDC\)có \(MD=BC\)và \(MD//BC.\)
\(\Rightarrow\)Tứ giác \(BMDC\)là hình bình hành.
\(\Rightarrow MC\)và \(BD\)là hai đường chéo của hình bình hành \(BMDC.\)
\(\Rightarrow BD\)đi qua trung điểm của đoạn thẳng \(MC.\)
#Riin

Bạn tham khảo ở đây
Câu hỏi của Công chúa thủy tề - Toán lớp 7 - Học toán với OnlineMath

Ta có hình vẽ:
M N A B C D
a/ Xét tam giác AMN và tam giác CDN có:
MN = ND (GT)
\(\widehat{ANM}=\widehat{CND}\) (đối đỉnh)
AN = NC (GT)
=> tam giác AMN = tam giác CDN (c.g.c)
Ta có: tam giác AMN = tam giác CDN
=> AM = CD (2 cạnh tương ứng)
Ta có: AM = MB (GT) (1)
Ta có: AM = CD (đã chứng minh trên) (2)
Từ (1), (2) => MB = CD (đpcm)
b/ Ta có: tam giác AMN = tam giác CDN (đã chứng minh trên)
=> \(\widehat{MAN}=\widehat{DCN}\) (2 góc tương ứng)
Mà 2 góc này đang ở vị trí so le trong nên
=> AM // CD
Vì A,M,B thẳng hàng nên MB // CD
=> \(\widehat{BMC}=\widehat{MCD}\) (so le trong) (1)
Ta có: BM = CD (đã chứng minh trên) (2)
MC: cạnh chung (3)
Từ (1),(2),(3) => tam giác BMC = tam giác DMC
=> \(\widehat{DMC}=\widehat{MCB}\) (2 góc tương ứng)
Mà 2 góc này đang ở vị trí so le trong
=> MN // BC (đpcm)

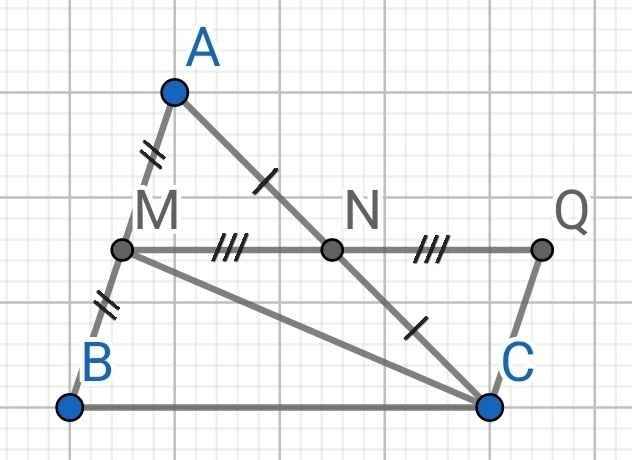
a) Xét ∆AMN và ∆CQN có:
AN = NC (do N là trung điểm của AC)
∠ANM = ∠CNQ (đối đỉnh)
NM = NQ (gt)
⇒ ∆AMN = ∆CQN (c-g-c)
b) Do ∆AMN = ∆CQN (cmt)
⇒ ∠MAN = ∠NCQ (hai góc tương ứng)
Mà ∠MAN và ∠NCQ là hai góc so le trong
⇒ AM // CQ
⇒ MB // CQ
c) Do ∆AMN = ∆CQN (cmt)
⇒ AM = CQ (hai cạnh tương ứng)
Mà AM = MB (do M là trung điểm của AB)
⇒ MB = CQ
Do BM // CQ (cmt)
⇒ ∠BMC = ∠QCM (so le trong)
Xét ∆BMC và ∆QCM có:
BM = CQ (cmt)
∠BMC = ∠QCM (cmt)
CM là cạnh chung
⇒ ∆BMC = ∆QCM (c-g-c)
⇒ BC = MQ (hai cạnh tương ứng)
Do NM = NQ (gt)
⇒ MN = 1/2 MQ
Mà BC = MQ (cmt)
⇒ MN = 1/2 BC
Sao MB // NG??