
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,Áp dụng tính chất tổng ba góc trong 1 tam giác vào \(\Delta ABC\),có:
\(180^o=\widehat{A}+\widehat{B}+\widehat{C}\)
\(\Rightarrow\widehat{C}=180^o-(\widehat{A}+\widehat{B})\)
\(=180^o-140^o\)
\(=40^o\)
Vậy \(\widehat{C}=40^o\)
b,Vì \(\widehat{A}>\widehat{B}=\widehat{C}\left(100^o>40^o=40^o\right)\)
\(\Rightarrow BC>AC=AB\)(Quan hệ giữa góc và cạnh đối diện )
Vậy BC là cạnh lớn nhất của tam giác ABC
c, Vì G là trọng tâm của tam giác ABC
\(\Rightarrow AG=\frac{2}{3}AM\)
\(\Rightarrow AM=AG:\frac{2}{3}\)
\(\Rightarrow AM=8.\frac{3}{2}\)
\(\Rightarrow AM=12\left(cm\right)\)
Vậy AM=12 cm
k mik nha !
sorry mik vẽ hình ko đc chuẩn lắm thông cảm nha

2:
a: Xét ΔABC có BM,CN là trung tuyến và G là giao của BM,CN
nên G là trọng tâm
=>BG=2GM và CG=2GN
=>BG=GE và CG=GF
=>G là trung điểm chung của BE và CF
=>BCEF là hình bình hành
=>BC=EF
b: Xét ΔFAE và ΔBGC có
FA=BG
AE=GC
FE=BC
=>ΔFAE=ΔBGC

a) Xét \(\Delta AMC\)và \(\Delta DMB\),ta có :
AM = DM(gt)
\(\widehat{M_1}=\widehat{M_2}\)(đối đỉnh)
CM = BM(vì M là trung điểm của BC)
=> \(\Delta AMC=\Delta DMB\left(c.g.c\right)\)
=> \(\widehat{C}=\widehat{B_1}\)(hai góc tương ứng)
AC = BD(hai cạnh tương ứng)
Khi đó \(\widehat{ABD}=\widehat{B_1}+\widehat{B_2}=\widehat{B_1}+\widehat{C}=90^0\)
Vậy góc ABD = 900
b) Xét \(\Delta ABC\)và \(\Delta BAD\)có :
AB chung
AC = BD(cmt)
=> \(\Delta ABC=\Delta BAD\)(hai cạnh góc vuông)
c) Từ kết quả câu b)
=> BC = AD = 2AM <=> \(AM=\frac{1}{2}BC\)
Em kiểm tra lại đề bài nhé! Trên tia đối tia AM hay tia đối tia MA ?
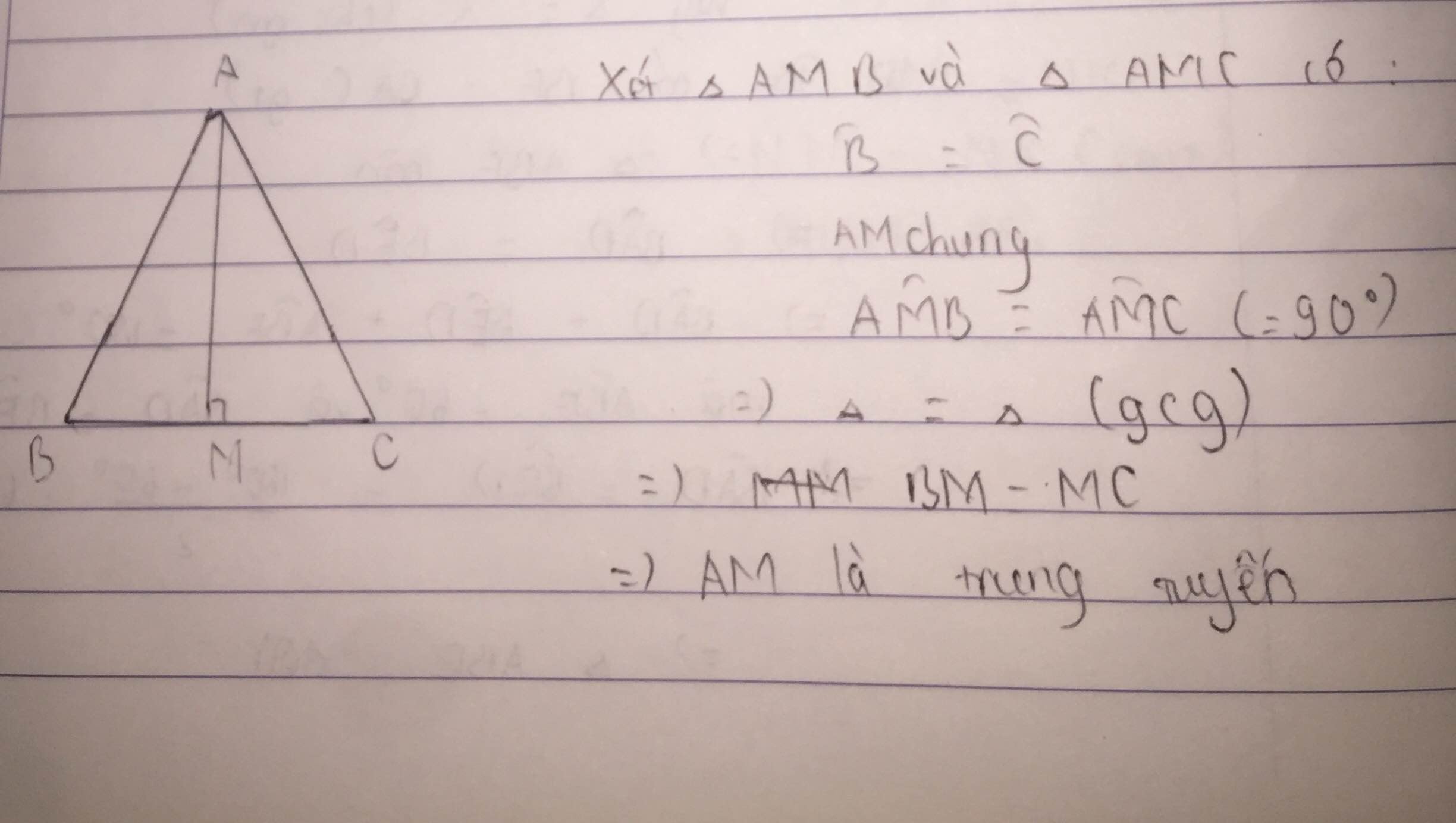
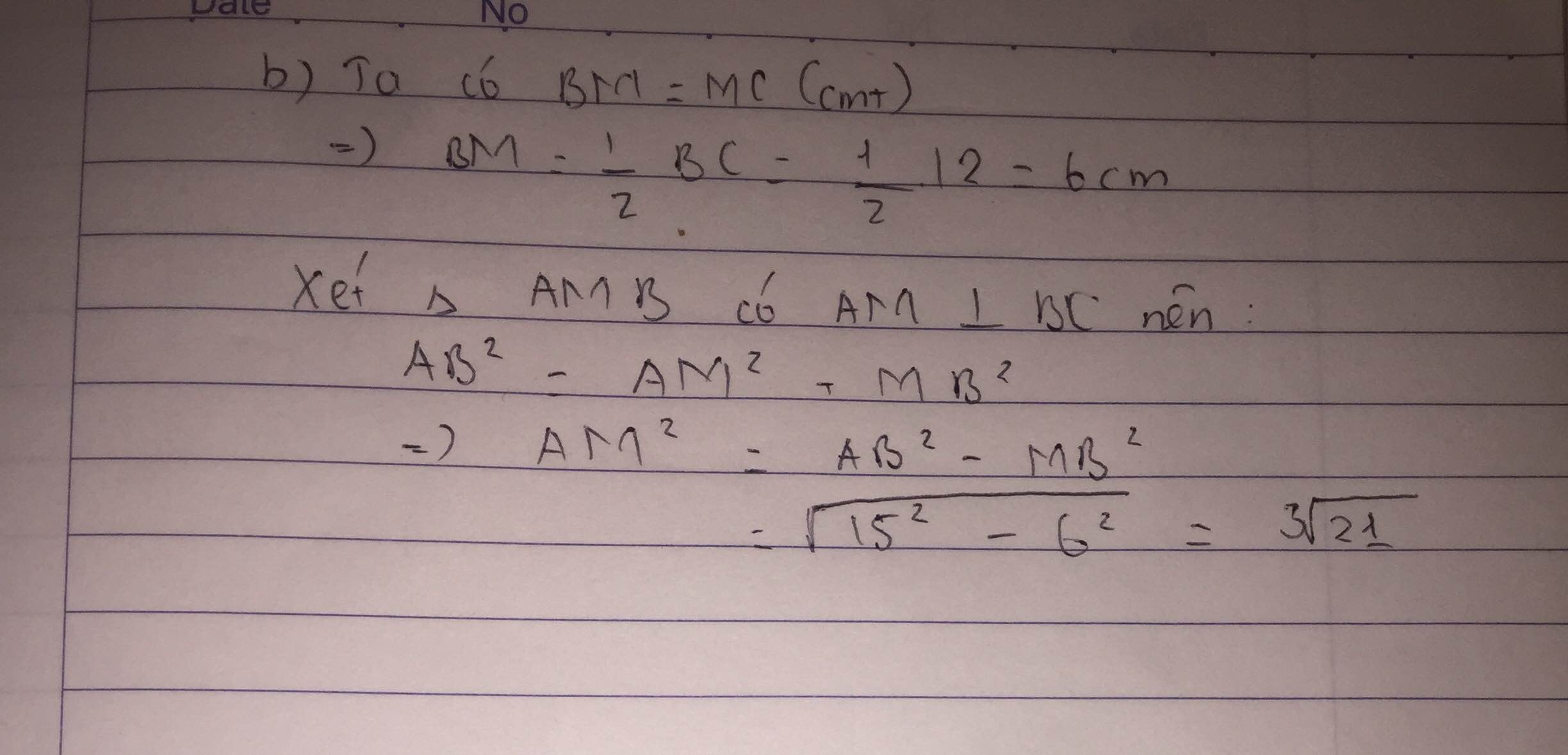
Góc AM?? Mình tính luôn ^AMB và ^AMC nhé !
Xét \(\Delta ABC\)có \(\widehat{BAC}+\widehat{B}+\widehat{C}=180^o\)(theo định lý tổng 3 góc trong của 1 tam giác)
\(\Rightarrow\widehat{BAC}+30^o+15^o=180^o\)
\(\Rightarrow\widehat{BAC}=135^o\)
Vì AM là đường trung tuyến của \(\widehat{BAC}\)
\(\Rightarrow\widehat{MAB}=\widehat{MAC}=\frac{\widehat{BAC}}{2}=\frac{135^o}{2}=67,5^o\)
Xét \(\Delta AMB\)có : \(\widehat{MAB}+\widehat{B}+\widehat{AMB}=180^o\)(đ/lý tổng 3 góc trong của 1 tam giác)
\(\Rightarrow67,5^o+30^o+\widehat{AMB}=180^o\)
\(\Rightarrow\widehat{AMB}=82,5^o\)
\(\Rightarrow\widehat{AMC}=180^o-\widehat{AMB}=180^o-82,5^o=97,5^o\)(Vì \(\widehat{AMB}+\widehat{AMC}=180^o\))
Trên mặt phẳng bờ BC chưa A lấy điểm N sao cho \(\Delta\)NCM đều
=> ^CMN = 60 độ
=> ^NMB = 120 độ
Mà NM = MC = BM
=> \(\Delta\)NMB cân tại tại B => ^NBM = 30 độ=> ^CBN = 30 độ mà ^CBA = 30 độ
=> M; A; N thẳng hàng
Xét \(\Delta\)CBN có: ^NCB = 60 độ ; ^CBN = 30 độ
=> ^CNB = 90 độ
=> ^CNA = 90 độ
mà ^ACN = ^MCN - ^MCA = 45 độ
=> \(\Delta\)NCA vuông cân tại N
=> NC = NA mà NC = NM
=> NA = NM => \(\Delta\)NAM cân tại N có: ^MNA = 30 độ => ^NMA = ^NAM = ( 180 - 30 ) : 2 = 75 độ
=> ^CAM = ^NAM - ^NAC = 75 - 45 = 30 độ
=> ^NAB = 180 - 30 - 15 - 30 = 105 độ