Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

muốn giúp lắm nhưng mới lớp 7 chỉ bt làm phần a,d nghĩ bài a,d là toán lớp 7

a) tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AE.AB=AH^2\)
tam giác AHC vuông tại H có đường cao HF nên áp dụng hệ thức lượng
\(\Rightarrow AF.AC=AH^2=AE.AB\)
b) \(AE.AB=AF.AC\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AE}{AC}=\dfrac{AF}{AB}\\\angle BACchung\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c-g-c\right)\)
c) Ta có: \(AH^4=AH^2.AH^2=AE.AB.AF.AC\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB.AC=AH.BC\)
\(\Rightarrow AH^4=AE.AF.BC.AH\Rightarrow AH^3=AE.AF.BC\)
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
b) Ta có: \(AE\cdot AB=AF\cdot AC\)
nên \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAFE vuông tại A và ΔABC vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
Do đó: ΔAFE\(\sim\)ΔABC(c-g-c)

b) xét ∆ABC có AD là đường phân giác của góc A
=>BD/AB=DC/AC ( tính chất)
Áp dụng tính chất dãy tỉ số bằng nhau , được :
BD/AB=DC/AC=BD/6=DC/8=(BD+DC)/(6+8)=BD/14=10/14=5/7
==>BD=6×5:7≈4,3
==>DC=10-4,3≈5,7
a,Áp dụng định lý Pi-ta-go vào tam giác ABC => tam giác ABC vuông tại A=> AH vuông góc vs BC
=> tam giác ABC đồng dạng vs tam giác HAC ( g.c.g)
b, Vì tam giác ABC vuông tại A nên ta có hệ thức: AC2=BC . HC => đpcm
c, có AD là tia phân giác của tam giác ABC => BD=CD=BC/2= 5cm

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64\)
=>AC=8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\\BH=\dfrac{6^2}{10}=3,6\left(cm\right)\end{matrix}\right.\)
b: ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra AE*AB=AF*AC
=>AE/AC=AF/AB
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
AE/AC=AF/AB
Do đó: ΔAEF đồng dạng với ΔACB
c: Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AB}{AD}=\dfrac{CB}{CD}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{AD}=\dfrac{CB}{CD}=\dfrac{AB+BC}{AD+CD}=\dfrac{AB+BC}{AC}\)(1)
ΔBAD vuông tại A có
\(cotABD=\dfrac{AB}{AD}\)(2)
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\widehat{DBC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(cotDBC=\dfrac{AB+BC}{AC}\)

a, Áp dụng hệ thức giữa cạnh và đường cao trong các tam giác vuông

∆AHC và ∆AHB ta có:
AE.AC = A H 2 = AD.AB => ∆AHC ~ ∆AHB(c.g.c)
b. Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ∆ABC tính được AH = 3cm => DE = 3cm
Trong ∆AHB vuông ta có:
tan A B C ^ = A H H B => A B C ^ ≈ 56 0 , S A D E = 27 13 c m 2

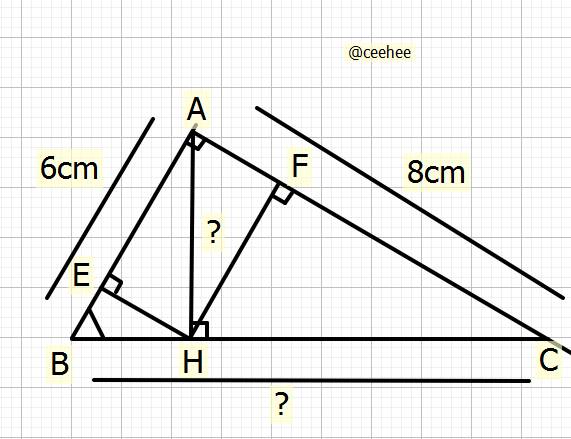
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)

1: BA=căn 10^2-6^2=8cm
sin ABC=AC/BC=3/5
=>góc ABC=37 độ
AH=6*8/10=4,8cm
BH=BA^2/BC=8^2/10=6,4cm
2: ΔAHB vuông tại H có HI là đường cao
nên AI*AB=AH^2
ΔAHC vuông tại H có HK là đường cao
nên AK*AC=AH^2
=>AI*AB=AK*AC
3: AI*AB=AK*AC
=>AI/AC=AK/AB
Xét ΔAIK và ΔACB có
AI/AC=AK/AB
góc IAK chung
=>ΔAIK đồng dạng với ΔACB

a, BC=BH+HC=8BC=BH+HC=8
Áp dụng HTL:
⎧⎪⎨⎪⎩AB2=BH⋅BC=16AC2=CH⋅BC=48AH2=CH⋅BC=12⇒⎧⎪ ⎪⎨⎪ ⎪⎩AB=4(cm)AC=4√3(cm)AH=2√3(cm){AB2=BH⋅BC=16AC2=CH⋅BC=48AH2=CH⋅BC=12⇒{AB=4(cm)AC=43(cm)AH=23(cm)
b,b, Vì K là trung điểm AC nên AK=12AC=2√3(cm)AK=12AC=23(cm)
Ta có tanˆAKB=ABAK=42√3=2√33≈tan490tanAKB^=ABAK=423=233≈tan490
⇒ˆAKB≈490