Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tam giác ABC có MN//BC nên \(\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)(định lý Thales)
\(\frac{AM}{AB}=\frac{AN}{AC}\Rightarrow\frac{5}{15}=\frac{AN}{12}\Rightarrow AN=\frac{5.12}{15}=4\)
\(\frac{AM}{AB}=\frac{MN}{BC}\Rightarrow\frac{5}{15}=\frac{MN}{20}\Rightarrow MN=\frac{5.20}{15}=\frac{20}{3}\)
Dễ thấy MNPB là hình bình hành nên \(MN=BP=\frac{20}{3}\)
Vậy \(AN=4\);\(MN=BP=\frac{20}{3}\)

a) Do MN//BC nên theo hệ quả của ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{MN}{BC}\)
\(\Rightarrow\) \(\dfrac{2}{4}\) = \(\dfrac{MN}{6}\)\(\Rightarrow\) MN = \(\dfrac{2\times6}{4}\)\(\Rightarrow\) MN = 3 cm
b) Do MN//BC nên theo ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{AN}{AC}\)
\(\Rightarrow\)\(\dfrac{12}{15}\)=\(\dfrac{AN}{18}\)\(\Rightarrow\) AN = \(\dfrac{12\times18}{15}\) = 14,4 cm


a) Vì n thuộc AC nên \(AN+NC=AC\)
Thay số: AN + 8 = 12
\(\Rightarrow AN=12-8=4\left(cm\right)\)
Ta có: \(\frac{AM}{AB}=\frac{5}{15}=\frac{1}{3}\)và \(\frac{AN}{AC}=\frac{4}{12}=\frac{1}{3}\)
\(\Rightarrow\frac{AM}{AB}=\frac{AN}{AC}\)
Áp dụng định lý Thales đảo suy ra MN // BC (đpcm)
b) Vì MN //BC (cmt) nên áp dụng định lý Thales, ta có:
\(\frac{AM}{AB}=\frac{MN}{BC}\Rightarrow\frac{MN}{20}=\frac{1}{3}\Rightarrow MN=\frac{20}{3}\)
Vậy MN = \(\frac{20}{3}\)

Xét \(\Delta ABC:MN//BC\left(gt\right).\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(Talet\right).\\ \Rightarrow\dfrac{5}{8}=\dfrac{AN}{10}.\\ \Rightarrow AN=6,25\left(cm\right).\)

Xét ΔABC có MN//BC
nên AM/AB=AN/AC
=>AN/20=4/20=1/5
nên AN=4(cm)

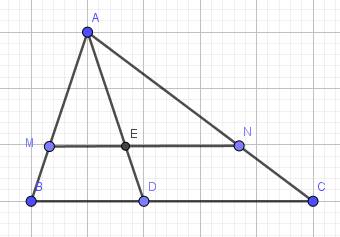
\(\Delta ABC\) có:
\(\dfrac{AM}{AB}=\dfrac{8}{12}=\dfrac{2}{3}\)
\(\dfrac{AN}{AC}=\dfrac{12}{15}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{2}{3}\)
\(\Rightarrow\) MN // BC (định lý Ta-lét)
\(\Delta AME\) và \(\Delta ABD\) có:
ME // BD (do MN // BC)
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AM}{AB}=\dfrac{2}{3}\) (hệ quả của định lý Ta-lét)

Vì MN//BC
=>\(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)<=>\(\dfrac{AN}{12}=\dfrac{5}{15}\)<=>AN=\(\dfrac{5.12}{15}\)<=>AN=4 (cm)
Vì NQ//AC
=>\(\dfrac{QC}{BC}=\dfrac{NA}{AB}\)<=>\(\dfrac{QC}{20}=\dfrac{4}{12}\)<=>QC=\(\dfrac{4.20}{12}\)<=>QC=\(\dfrac{20}{3}\) (cm)
=>BQ = BC - QC =20 - \(\dfrac{20}{3}\)=\(\dfrac{40}{3}\)(cm)
chúc bạn học tốt!