Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)
do tam giác ABC vuông tại A , mà ta có : D nằm giữa A , B , suy ra : AD + DB = AB
suy ra : 3 + DB = 4
suy ra : DB = 4-3=1 (cm)
Theo giả thiết ta có : AC =3 (cm)
và AB = 3 (cm)
suy ra : tam gác : ADC vuông cân tại A
vậy : góc ACD = góc ADC ( 2 góc ở đáy bằng nhau )
c )
nối M với D
Xét tam giác ADM và tam giác ACM có :
góc DAM = góc CAM ( AM tia p/g của góc A )
AM cạnh chung
AB = AC ( c/m câu a )
suy ra : tam giác ADM = tam giác ACM ( c-g-c)
suy ra :MD = MC ( 2 cạnh tương ứng )
xin lỗi nha tui ms làm đc vậy thôi mà không biết có đúng ko nữa
nếu sai thì xl bn nha
ngu
a) xét tam giác abc có bc^2=ac^2+ab^2 (định lý pi-ta-go )
5^2=3^2+4^2
25=9+16
vậy tam giác abc là tam giác vuông
2 câu còn lại tự túc

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔACD có AC=AD
nên ΔACD cân tại A
=>góc ACD=góc ADC
c: Xét ΔADM và ΔACM có
AD=AC
góc DAM=góc CAM
AM chung
DO đo: ΔADM=ΔACM
=>MD=MC

a: Xét ΔABD và ΔAMD có
AB=AM
góc BAD=góc MAD
AD chung
Do đó; ΔABD=ΔAMD
b: Xét ΔDBN và ΔDMC có
góc DBN=góc DMC
DB=DM
góc BDN=góc MDC
Do đó; ΔDBN=ΔDMC
=>BN=MC
c: Xét ΔANC có AB/BN=AM/MC
nên BM//CN

a: BC=8cm
BC>AC
=>góc A>góc B
b: XétΔABD có
AC vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
c: GB+2GC=GB+GA>AB

a. Xét tam giác vuông ABC
Theo định lý Py - ta - go ta có :
AB2 + AC2 = BC2
=> 32 + AC2 = 52
=> 9 + AC2 = 25
=> AC2 = 16
=> AC = 4
Vậy AB < AC < BC
b. Xét tam giác BAM và tam giác BDM ta có :
BM chung
Góc BAM = góc BDM ( = 90 độ )
BA = BD ( gt)
=> tam giác BAM = tam giác BDM ( ch - cgv)
=> MA = MD ( hai cạnh tương ứng )
Xét tam giác AMN và tam giác DMC
góc AMN = góc DMC ( đối đỉnh )
MA = MD ( cmt)
góc MAN= góc MDC ( = 90 độ )
=> Tam giác AMN = tam giác DMC
=> MN = MC
=> Tam giác MNC cân

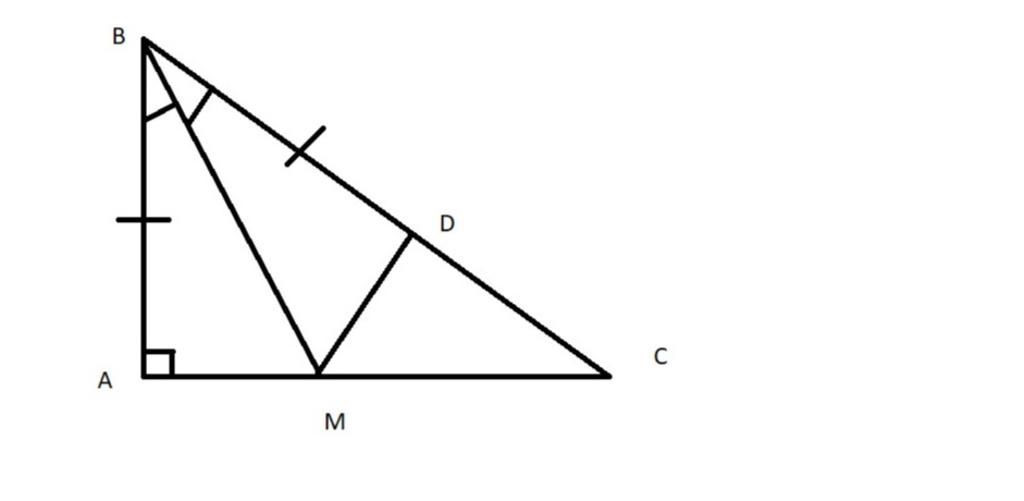

a)Xét △ABM và △△ DBM , ta có :
AB=BD(gt)
ˆABM^ == ˆDBM^ ( vì BM là tia phân giác của ˆABC^ )
BM là chung
⇒ △△ ABM= △△ DBM(c−g−c)
b)Ta có : ˆBAM^ == ˆBDM (( vì △ ABM= △ DBM)
Mà ˆBAM^ =90o(=90) ( vì △ ABC vuông tại A)
⇒⇒ ˆBDM=90o
⇒MD⇒ ⊥⊥ BC
c) Vì MD⊥⊥ BC(cmt)
⇒ ˆMDC^ =90o=90
⇒ △ MDC vuông tại D
⇒MC>MD(ch>cgv)
Mà MD=MA( vì △ABM=△ DBM)
⇒MC>MA

a. Xét tam giác ABM và tam giác DBM :
BM chung
Góc ABM =góc DBM ( gt)
BD = BA (gt)
=> Tam giác ABM = tam giác DBM ( ch-gn)
b) Ta có tam giác ABM = tam giác DBM
=> Góc BAM = góc BDM ( = 90 độ)
=> MD vuông góc với BC
c) Xét tam giác vuông DMC vuông tại D ta có :
MC > MD ( vì MC là cạnh huyền )
Mà MD = MA
=> MC > MA

