Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

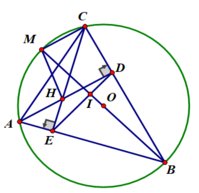
c) Do tứ giác AEDC là tứ giác nội tiếp nên ∠(CAB) = ∠(IDB) (cùng bù ∠(CDE) )
Mặt khác ∠(CAB) = ∠(CMB) (2 góc nội tiếp cùng chắn cung BC)
⇒ ∠(CMB) = ∠(IDB)
⇒ Tứ giác CMID là tứ giác nội tiếp ( Góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó)

a) Xét tứ giác AEDC có
\(\widehat{AEC}=\widehat{ADC}\left(=90^0\right)\)
\(\widehat{AEC}\) và \(\widehat{ADC}\) là hai góc cùng nhìn cạnh AC
Do đó: AEDC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

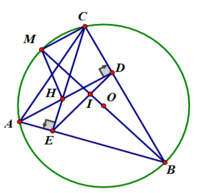
b) Xét ΔABD và Δ CEB có:
∠(ABC) chung
∠(ADB) = ∠(CEB) = 90 0
⇒ ΔABD ∼ Δ CBE (g.g)
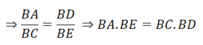

a) Xét tứ giác BNHM có
\(\widehat{BNH}\) và \(\widehat{BMH}\) là hai góc đối
\(\widehat{BNH}+\widehat{BMH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BNHM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a) Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}\left(=90^0\right)\)
nên AEDB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a) Xét tứ giác AEDC có:
∠(AEC) = ∠(ADC) = 90 0
Mà 2 góc này cùng nhìn cạnh AC
⇒ Tứ giác AEDC là tứ giác nội tiếp