Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ACHE có
HE//AC
HE=AC
Do đó: ACHE là hình bình hành
b: Ta có: ACHE là hình bình hành
nên AE//HC và AE=HC
=>AE//HB và AE=HB
Xét tứ giác AEBH có
AE//BH
AE=BH
Do đó: AEBH là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AEBH là hình chữ nhật

a:
AB\(\perp\)AC
AB//CD
Do đó: CA\(\perp\)CD
Xét ΔABI vuông tại A và ΔCDI vuông tại C có
IA=IC
\(\widehat{AIB}=\widehat{CID}\)
Do đó:ΔABI=ΔCDI
=>AB=CD và IB=ID
Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
b: HK\(\perp\)AB
AC\(\perp\)AB
Do đó: HK//AC
Xét tứ giác AHKI có
AH//KI
AI//HK
Do đó: AHKI là hình bình hành
mà \(\widehat{IAH}=90^0\)
nên AHKI là hình chữ nhật
=>AK=HI

a: góc DFB=góc ACB
góc DBF=góc ACB
=>góc DFB=góc DBF
=>ΔDBF cân tại D
b: Xét tứ giác DCEF có
DF//CE
DF=CE
=>DCEF là hình bình hành

a: Xét tứ giác AECH có
AE//CH
AH//CE
Do đó: AECH là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AECH là hình chữ nhật

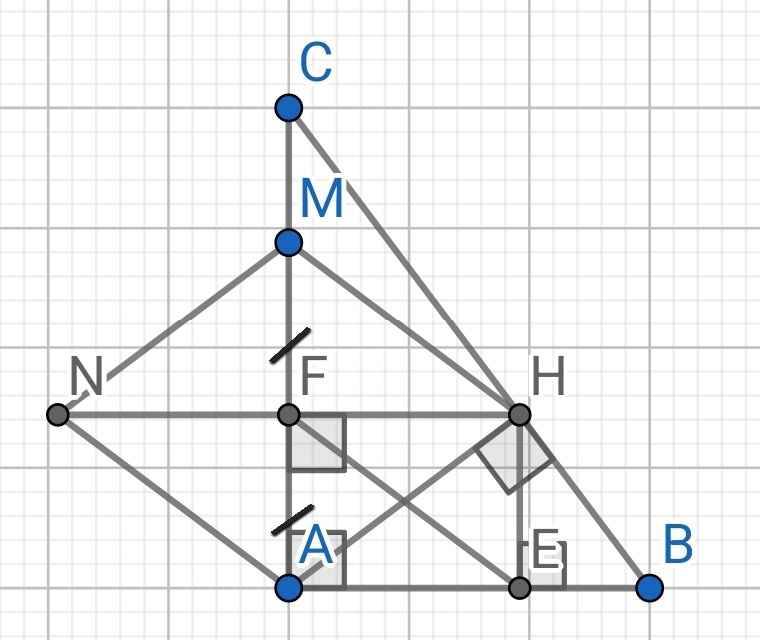 a) Do HE AB (gt)
a) Do HE AB (gt)
⇒ ∠AEH = 90⁰
Do HF AC (gt)
⇒ ∠AFH = 90⁰
Do ABC vuông tại A (gt)
⇒ ∠FAE = 90⁰
Tứ giác AEHF có:
∠AFH = ∠AEH = ∠FAE = 90⁰
⇒ AEHF là hình chữ nhật
b) Do AEHF là hình chữ nhật (cmt)
⇒ AF // HE và AF = HE
⇒ FM // HE
Do M và A đối xứng nhau qua F
F là trung điểm của AM
⇒ FM = AF
Mà AF = HE (cmt)
⇒ FM = HE
Tứ giác EFMH có:
FM // HE (cmt)
FM = HE (cmt)
⇒ EFMH là hình bình hành
c) Do MN // AH (gt)
⇒ ∠NMF = ∠FAH (so le trong)
Xét hai tam giác vuông: ∆MNF và ∆AHF có:
FM = AF (cmt)
∠NMF = ∠FAH (cmt)
⇒ ∆MNF = ∆AHF (cạnh góc vuông - góc nhọn kề)
⇒ MN = AH (hai cạnh tương ứng)
Tứ giác AHMN có:
MN // AH (gt)
MN = AH (cmt)
⇒ AHMN là hình bình hành
Mà AM ⊥ HN (HF ⊥ AC)
⇒ AHMN là hình thoi

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

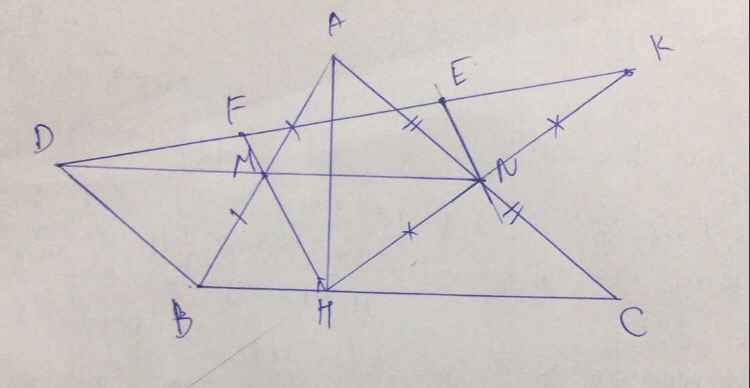
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
Xét tứ giác BDNC có
DN//BC
BD//NC
Do đó: BDNC là hình bình hành
b: Xét tứ giác BDNH có BH//DN
nên BDNH là hình thang
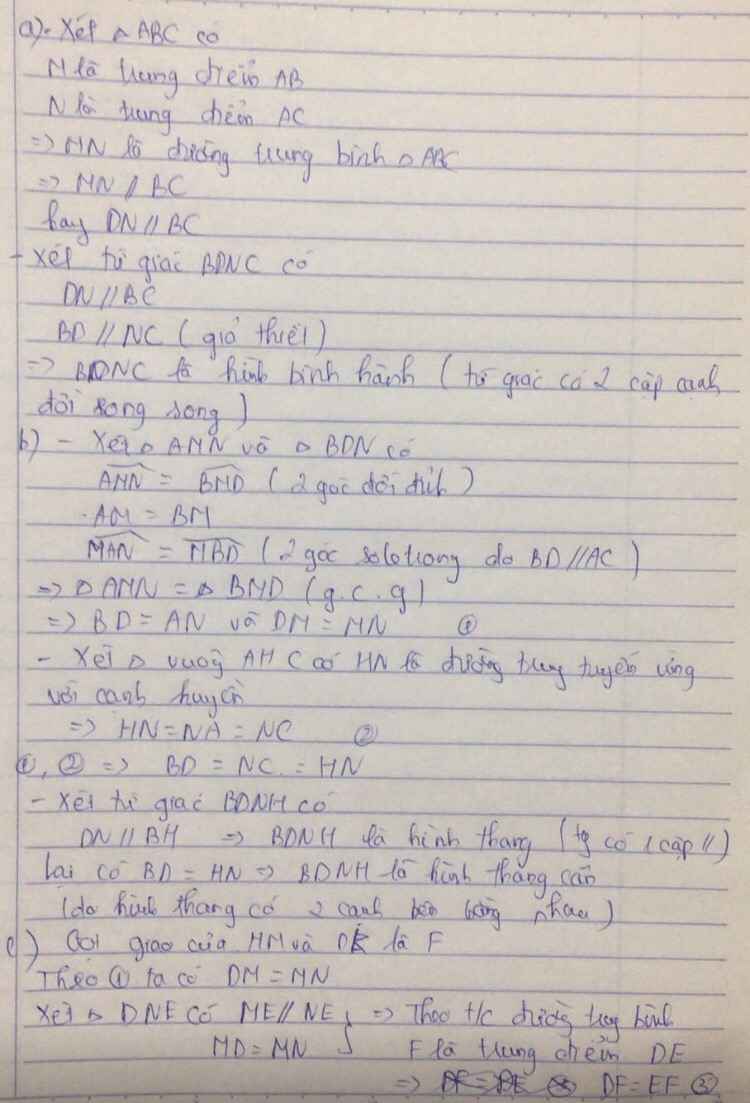
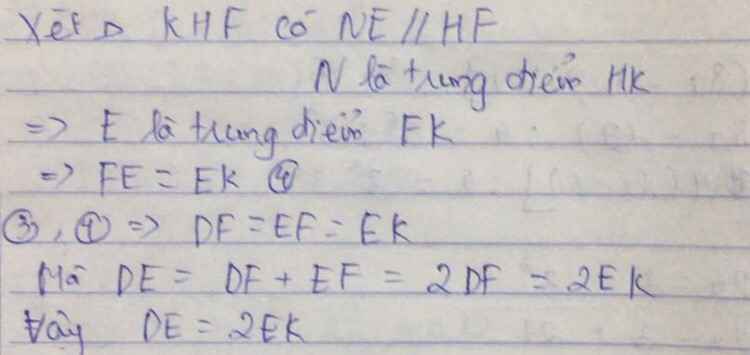
a: Xét tứ giác ACHE có
EH//AC
EH=AC
Do đó: ACHE là hình bình hành
b: Xét tứ giác AHBE có
AE//BH(vì AE//CH)
AE=BH(=CH)
Do đó: AHBE là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBE là hình chữ nhật