

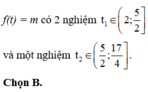
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


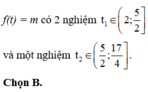

Đặt t = t ( x ) = 2 x + 2 - x với x ∈ [ - 1 ; 2 ]
Hàm t=t(x) liên tục trên [-1;2] và
t ' ( x ) = 2 x ln 2 - 2 - x ln 2 , t ' ( x ) = 0 ⇔ x = 0
Bảng biến thiên

Vậy x ∈ [ - 1 ; 2 ] ⇒ t ∈ 2 ; 17 4
Với mỗi t ∈ ( 2 ; 5 2 ] có 2 giá trị của x thỏa mãn t = 2 x + 2 - x
Với mỗi t ∈ 2 ∪ 5 2 ; 17 4 có duy nhất 1 giá trị x thỏa mãn.
Xét phương trình f(t)=m với t ∈ 2 ; 17 4
Từ đồ thị, phương trình f ( 2 x + 2 - x ) = m có số nghiệm nhiều nhất khi và chỉ khi phương trình f(t)=m có 2 nghiệm t 1 , t 2 , trong đó có t 1 ∈ ( 2 ; 5 2 ] , t 2 ∈ ( 5 2 ; 17 4 ]
Khi đó, phương trình có nhiều nhất 3 nghiệm phân biệt thuộc đoạn [-1;2]
Chọn đáp án B.

Chọn B
Đặt t = x 2 - 2 x với x ∈ - 3 2 ; 7 2
Bảng biến thiên của hàm số t = x 2 - 2 x trên đoạn - 3 2 ; 7 2 là:
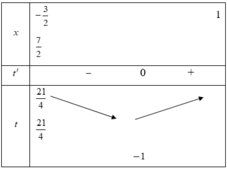
Dựa vào bảng biến thiên t ∈ - 1 ; 21 4
Khi đó phương trình f ( x 2 - 2 x ) = m (1) trở thành f(t)=m (2).
Ta thấy, với mỗi giá trị t ∈ ( - 1 ; 21 4 ] ta tìm được hai giá trị của x ∈ - 3 2 ; 7 2
Do đó, phương trình (1) có 4 nghiệm thực phân biệt thuộc - 3 2 ; 7 2 khi và chỉ khi phương trình (2) có hai nghiệm thực phân biệt thuộc ( - 1 ; 21 3 ]
Đường thẳng y=m cắt đồ thị hàm số y=f(t) tại hai điểm phân biệt có hoành độ thuộc - 1 ; 21 4
Dựa vào đồ thị ta thấy chỉ có hai giá trị nguyên của m thỏa yêu cầu là m=3 và m=5