Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Khi m = -4 thì:
\(x^2-5x+\left(-4\right)-2=0\)
\(\Leftrightarrow x^2-5x-6=0\)
\(\Delta=\left(-5\right)^2-5\cdot1\cdot\left(-6\right)=49\Rightarrow\sqrt{\Delta}=\sqrt{49}=7>0\)
Pt có 2 nghiệm phân biệt:
\(x_1=\dfrac{5+7}{2}=6;x_2=\dfrac{5-7}{2}=-1\)

Tìm max chứ nhể ???
Có : \(\Delta'=m^2+m\)
Pt có 2 nghiệm p/b thì \(\Delta'=m^2+m>0\Leftrightarrow\orbr{\begin{cases}m< -1\\m>0\end{cases}}\)
Theo hệ thức Vi-ét \(\hept{\begin{cases}x_1+x_2=2m\\x_1x_2=-m\end{cases}}\)
Vì x1; x2 là nghiệm của pt nên \(\hept{\begin{cases}x_1^2-2mx_1-m=0\\x_2^2-2mx_2-m=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}2mx_1=x_1^2-m\\2mx_2=x_2^2-m\end{cases}}\)
Ta có : \(T=\frac{1}{x_1^2+2mx_2+11\left(m+1\right)}+\frac{1}{x_2^2+2mx_1+11\left(m+1\right)}\)
\(=\frac{1}{x_1^2+x_2^2-m+11m+11}+\frac{1}{x_2^2+x_1^2-m+11m+11}\)
\(=\frac{1}{\left(x_1+x_2\right)^2-2x_1x_2+10m+11}+\frac{1}{\left(x_1+x_2\right)^2-2x_1x_2+10m+11}\)
\(=\frac{2}{\left(x_1+x_2\right)^2-2x_1x_2+10m+11}\)
\(=\frac{2}{4m^2+2m+10m+11}\)
\(=\frac{2}{4m^2+12m+11}\)
\(=\frac{2}{\left(4m^2+12m+9\right)+2}\)
\(=\frac{2}{\left(2m+3\right)^2+2}\le\frac{2}{2}=1\)
Dấu "=" khi m = -3/2 (thỏa mãn)

a:Sửa đề: x^2-(m+1)x+2m-8=0
Khi m=2 thì (1) sẽ là x^2-3x-4=0
=>(x-4)(x+1)=0
=>x=4 hoặc x=-1
b: Δ=(-m-1)^2-4(2m-8)
=m^2+2m+1-8m+32
=m^2-6m+33
=(m-3)^2+24>=24>0
=>(1) luôn có hai nghiệm pb
\(x_1^2+x_2^2+\left(x_1-2\right)\left(x_2-2\right)=11\)
=>(x1+x2)^2-2x1x2+x1x2-2(x1+x2)+4=11
=>(m+1)^2-(2m-8)-2(m+1)+4=11
=>m^2+2m+1-2m+8-2m-2+4=11
=>m^2-2m=0
=>m=0 hoặc m=2

\(ac=-3< 0\Rightarrow\) pt đã cho luôn có 2 nghiệm pb trái dấu với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-3\end{matrix}\right.\)
\(\dfrac{x_1}{x_2^2}+\dfrac{x_2}{x_1^2}=m-1\Leftrightarrow\dfrac{x_1^3+x_2^3}{\left(x_1x_2\right)^2}=m-1\)
\(\Leftrightarrow\dfrac{\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)}{9}=m-1\)
\(\Leftrightarrow8\left(m-1\right)^3+18\left(m-1\right)=9\left(m-1\right)\)
\(\Leftrightarrow\left(m-1\right)\left[8\left(m-1\right)^2+9\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\8\left(m-1\right)^2+9=0\left(vô-nghiệm\right)\end{matrix}\right.\)

\(\Delta=\left(m-1\right)^2+8>0;\forall m\) nên pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-2\end{matrix}\right.\)
\(\left(1-\dfrac{2}{x_1+1}\right)^2+\left(1-\dfrac{2}{x_2+1}\right)^2=1\)
\(\Leftrightarrow\left(\dfrac{x_1-1}{x_1+1}\right)^2+\left(\dfrac{x_2-1}{x_2+1}\right)^2=1\)
\(\Leftrightarrow\left(\dfrac{x_1-1}{x_1+1}+\dfrac{x_2-1}{x_2+1}\right)^2-2\left(\dfrac{x_1-1}{x_1+1}\right)\left(\dfrac{x_2-1}{x_2+1}\right)=1\)
\(\Leftrightarrow\left(\dfrac{\left(x_1-1\right)\left(x_2+1\right)+\left(x_1+1\right)\left(x_2-1\right)}{\left(x_1+1\right)\left(x_2+1\right)}\right)^2-2\left(\dfrac{x_1x_2-\left(x_1+x_2\right)+1}{x_1x_2+x_1+x_2+1}\right)=1\)
\(\Leftrightarrow\left(\dfrac{2x_1x_2-2}{x_1x_2+x_1+x_2+1}\right)^2-2\left(\dfrac{x_1x_2-\left(x_1+x_2\right)+1}{x_1x_2+x_1+x_2+1}\right)=1\)
\(\Leftrightarrow\left(\dfrac{-6}{m-2}\right)^2+2\left(\dfrac{m}{m-2}\right)=1\)
\(\Leftrightarrow36\left(\dfrac{1}{m-2}\right)^2+4\left(\dfrac{1}{m-2}\right)+1=0\)
Pt trên vô nghiệm nên ko tồn tại m thỏa mãn yêu cầu
Tới đó đặt \(\dfrac{1}{m-2}=t\) là thành 1 pt bậc 2 bình thường, bấm máy thấy nó vô nghiệm là đủ kết luận rồi em
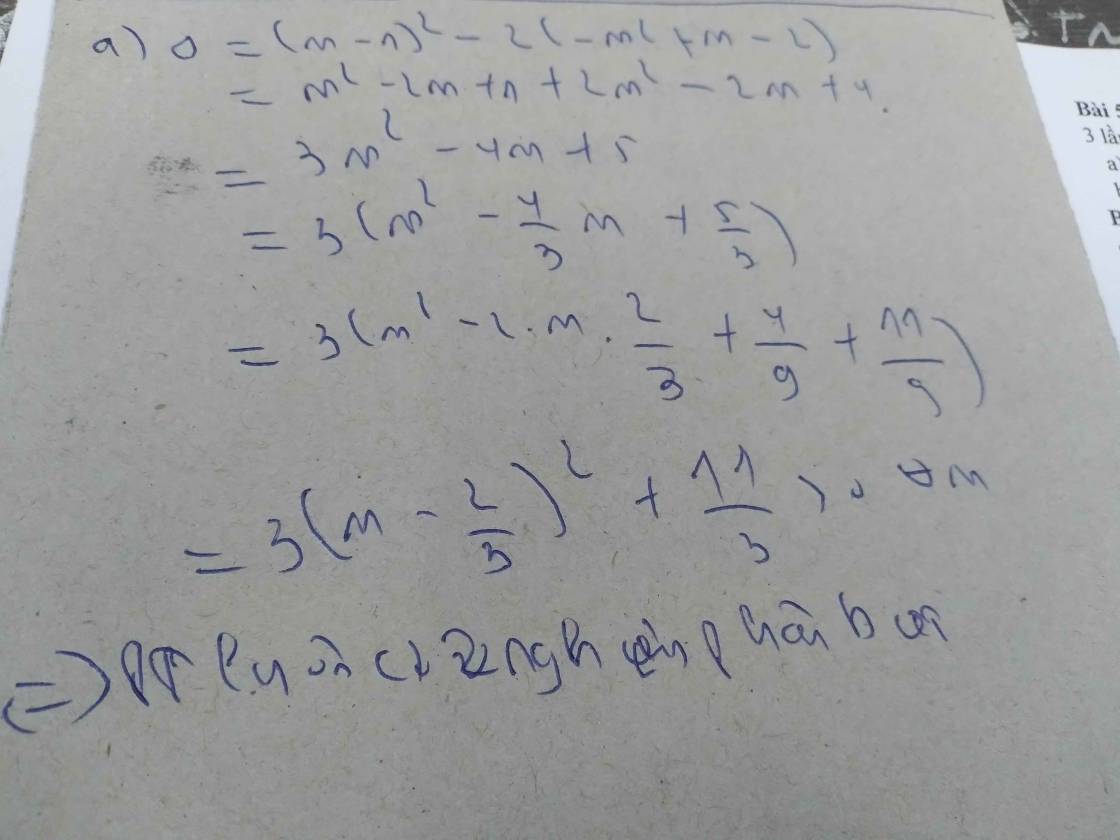
sao cho T đạt GTLN nha
a, Ta có x2- 2mx - m = 0 (1)
Với m=1 , (1)<=> x2- 2x-1=0
<=> x2-2x+1 -2 = 0
<=> (x-1)2=2
=>\(\left[{}\begin{matrix}x-1=-\sqrt{2}\\x-1=\sqrt{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{2}+1\\x=\sqrt{2}+1\end{matrix}\right.\)
b , câu b ko biết làm