Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(f\left(x\right)=m\left(x-1\right)^3\left(x^2-4\right)+x^4-3\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(f\left(1\right)=-2< 0\)
\(f\left(2\right)=13>0\)
\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc khoảng (1;2)
\(f\left(-2\right)=13>0\Rightarrow f\left(1\right).f\left(-2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc khoảng (-2;1)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 2 nghiệm phân biệt

Chứng minh rằng phương trình sau có ít nhất hai nghiệm :
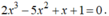
- Xét hàm số: f ( x ) = 2 x 3 - 5 x 2 + x + 1 là hàm đa thức.
⇒ Hàm số f liên tục trên R.
- Ta có:
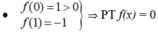 có ít nhất một nghiệm c1 ∈ (0;1).
có ít nhất một nghiệm c1 ∈ (0;1).
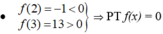 có ít nhất một nghiệm c2 ∈ (2;3).
có ít nhất một nghiệm c2 ∈ (2;3).
- Mà c ≠ c 2 nên PT f(x) = 0 có ít nhất 2 nghiệm.

Đề bài sai, ví dụ: với \(a=b=1\) thì \(x^2+x-1=0\) có 1 nghiệm thuộc \(\left(0;1\right)\) thỏa mãn yêu cầu
Nhưng \(x^2-2x+1=0\) có nghiệm kép, không phải hai nghiệm phân biệt