Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

số cách chọn 8 học sinh ừ 18 học sinh là :\(C^8_{18}\)
các TH:
thuộc 2 khối 10 và 11: \(C^8_{11}\)
thuộc 2 khói 11 và 12: \(C^8_{13}\)
thuộc 2 khối 13 và 10: \(C^8_{12}\)
=> số cách chọn theo đề là : 414811

Đáp án C.
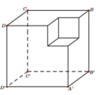
Mỗi mặt sẽ có 4 phần thuộc hình chỉ được tô một lần tức là mỗi mặt sẽ sinh ra 4 hình lập phương thỏa mãn yêu cầu bài toán, ta có 6 mặt, từ đó ta có 24 hình thỏa mãn yêu cầu.
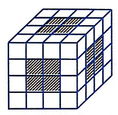

Đáp án D
Tổng số cách chọn 8 em từ đội 18 người là ![]()
Số cách chọn 8 em từ khối 12 và khối 11 là ![]()
Số cách chọn 8 em từ khối 11 và khối 10 là ![]()
Số cách chọn 8 em từ khối 10 và khối 12 là ![]()
Vậy số cách chọn để có các em ở cả 3 khối là
![]()

chọn 5 đội trong 12 đội có \(C^5_{12}=792\) cách
=> \(n\left(\Omega\right)=792\)
Gọi A:" 5 đội được chọn có ít nhất 1 đội cờ đỏ khối 10 và ít nhất 1 đội cờ đỏ khối 11 "
+) 1 đội K10 +4 đội K11 => có \(C^1_5.C^4_7=175\) cách
+) 2 đội K10 +3 đội K11 => có \(C^2_5.C^3_7=350\)cách
+) 3 đội k10 + 2 đội k11 => có \(C^3_5.C^2_7=210\) cách
+) 4 độ k10 + 1 đội k11 => có \(C^4_5.C^1_7=35\)cách
=> n(A) = 175+350+210+35 = 770
=> P(A) = 770/792=35/36

Chọn D
Gọi A là biến cố “Học sinh nhận được 6 điểm”.
Xác suất đánh đúng 1 câu là 1 4 và đánh sai 1 câu là 3 4 .
Để nhận được 6 điểm học sinh đó cần đánh đúng 12 câu và sai 8 câu.
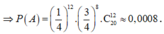

Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 13 quả bóng có \({C}_{13}^3 = 286\) cách.
\( \Rightarrow n\left( \Omega \right) = 286\)
a) Gọi \(A\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu xanh”, \(B\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu đỏ”, \(C\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu vàng”
Vậy \(A \cup B \cup C\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu”
Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 5 quả bóng xanh có \({C}_5^3 = 10\) cách.
\( \Rightarrow n\left( A \right) = 10 \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega\right)}} = \frac{{10}}{{286}} = \frac{5}{{143}}\)
Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 6 quả bóng đỏ có \({C}_6^3 = 20\) cách.
\( \Rightarrow n\left( B \right) = 20 \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{{20}}{{286}} = \frac{{10}}{{143}}\)
Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 2 quả bóng vàng có 0 cách.
\( \Rightarrow n\left( C \right) = 0 \Rightarrow P\left( C \right) = 0\)
\( \Rightarrow P\left( {A \cup B \cup C} \right) = P\left( A \right) + P\left( B \right) + P\left( C \right) = \frac{{15}}{{243}}\)
b) Gọi \(D\) là biến cố “Có đúng 2 quả bóng xanh trong 3 quả bóng lấy ra”
Vậy \(A \cup D\) là biến cố “Có ít nhất 2 quả bóng xanh trong 3 quả bóng lấy ra”
Chọn ngẫu nhiên từ hộp 2 quả bóng trong tổng số 5 quả bóng xanh có \({C}_5^2 = 10\) cách.
Chọn ngẫu nhiên từ hộp 1 quả bóng trong tổng số 8 quả bóng đỏ hoặc vàng có \({C}_8^1 = 8\) cách.
\( \Rightarrow n\left( D \right) = 10.8 = 80 \Rightarrow P\left( D \right) = \frac{{n\left( D \right)}}{{n\left( \Omega \right)}} = \frac{{80}}{{286}} = \frac{{40}}{{143}} \Rightarrow P\left( {A \cup D} \right) = P\left( A \right) + P\left( D \right) = \frac{{45}}{{143}}\)