Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: Đường tròn (O;R) có đường kính CD và điểm A nằm trên cung CD => ^CAD=900
=> ^PAQ=900 => \(\Delta\)APQ vuông tại A
Do PQ là tiếp tuyến của (O) tại B => AB là đường cao của \(\Delta\)APQ
=> ^PAB=^AQP (Cùng phụ ^APQ) hay ^CAO=^DQP
Mà \(\Delta\)AOC cân tại O => ^CAO=^ACO => ^DQP=^ACO
Lại có: ^ACO+^PCD=1800 => ^DQP+^PCD=1800
=> Tứ giác CPQD nội tiếp đường tròn (đpcm).
b) Xét \(\Delta\)APQ vuông tại A: Có đường trung tuyến AI => \(\Delta\)AIQ cân tại I
=> ^IAQ=^IQA hay ^IAQ=^DQP => ^IAQ=^ACO (Do ^DQP=^ACO)
Hay ^IAQ=^ACD. Mà ^IAQ+^CAI=900 => ^ACD+^CAI=900
=> AI vuông góc với CD (đpcm).
c) Ta thấy tứ giác CPQD nội tiếp đường tròn
=> 4 đường trung trực của CP;CD;DQ;PQ cắt nhau tại 1 điểm (1)
E là tâm đường tròn ngoại tiếp \(\Delta\)CPQ => Trung trực của CP và CD cắt nhau tại E (2)
Từ (1) và (2) => Điểm E nằm trên trung trực của PQ.
Lại có: I là trung điểm PQ => E là điểm cách PQ 1 khoảng bằng đoạn EI (*)
AB vuông góc PQ; EI cũng vuông góc PQ => AB//EI hay AO//EI (3)
E thuộc trung trực CD; O là trung điểm CD => OE vuông góc CD.
Mà AI vuông góc CD => OE//AI (4)ư
Từ (3) và (4) => Tứ giác AOEI là hình bình hành => AO=EI (**)
Từ (*) và (**) => E là điểm cách PQ 1 khoảng bằng đoạn AO
Mà AO là bk của (O); PQ là tiếp tuyến của (O) tại B
Nên ta có thể nói: Điểm E là điểm cách tiếp tuyến của (O) tại B một khoảng bằng độ dài bán kính của (O)
Vậy khi đường kính CD thay đổi thì điểm E di động trên đường thẳng song song với tiếp tuyến tại B của đường tròn (O) và cách (O) 1 khoảng bằng độ dài bk của (O).

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')

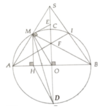
a, Chứng minh ∆MEF:∆MOA
b, ∆MEF:∆MOA mà AO=OM => ME=EF
c, Chứng minh F là trực tâm của ∆SAB, AI là đường cao, chứng minh A,I,F thẳng hàng
d, FA.SM = 2 R 2
e, S M H O = 1 2 OH.MH ≤ 1 2 . 1 2 M O 2 = 1 4 R 2
=> M ở chính giữa cung AC
a: góc EAF=90 độ, M là trung điểm của EF
=>MA=ME=MF
=>góc MAE=góc MEA
AC*AE=AD*AF
=>AC/AD=AF/AE
=>ΔACD đồng dạng với ΔAFE
=>góc ACD=góc AFE
AM cắt CD tại L
góc LCA+góc LAC=góc AEF+góc AFE=90 độ
=>AM vuông góc CD