Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét (O) có
ΔANB nội tiếp
AB là đường kính
Do đó: ΔANB vuông tại N
Xét ΔCAB có
AN,BM là các đường cao
AN cắt BM tại H
Do đó: H là trực tâm
=>CH vuông góc với AB
b: góc IMO=góc IMH+góc OMH
=90 độ-góc ACH+góc ABM
=90 độ
=>MI là tiếp tuyến của (O)

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
=>ΔAMB vuông tại M
Xét (O) có
ΔANB nội tiếp
AB là đường kính
=>ΔANB vuông tại N
Xét ΔCAB có
AN.BM là đường cao
AN cắt BM tại H
=>H là trực tâm
=>CH vuông góc AB
b:
Gọi giao của CH vơi AB là K
=>CH vuông góc AB tại K
góc OMI=góc OMH+góc IMH
=góc OBM+góc IHM
=góc OBM+góc BHK=90 độ
=>IM là tiếp tuyến của (O)

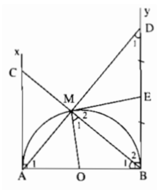
Tam giác EBM cân nên ∠ M 2 = ∠ B 2 . Suy ra ∠ M 1 + ∠ M 2 = ∠ B 1 + ∠ B 2 = 90 ° , tức là ME ⊥ OM tại M. Vậy ME là tiếp tuyến của nửa đường tròn.
a, HS tự chứng minh
b, Gọi CH ∩ AB = K
Chứng minh được ∆MIC cân tại I
=> I C M ^ = I M C ^
Tương tự: O M A ^ = O A M ^
Chứng minh được I M O ^ = 90 0 => ĐPCM