Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số vecto tạo từ 2n điểm là: \(A_{2n}^2\)
Đa giác đều 2n đỉnh có n đường chéo, cứ 2 đường chéo cho ta 1 hình chữ nhật tương ứng, do đó số hình chữ nhật có đỉnh là đỉnh của đa giác đều là: \(C_n^2\)
\(\Rightarrow A_{2n}^2=9C_n^2\Leftrightarrow\dfrac{\left(2n\right)!}{\left(2n-2\right)!}=\dfrac{9.n!}{2!.\left(n-2\right)!}\)
\(\Leftrightarrow2n\left(2n-1\right)=\dfrac{9n\left(n-1\right)}{2}\)
\(\Leftrightarrow n=5\)
dạ em chưa hiểu tại sao số vecto tạo từ 2n điểm và số hình chữ nhật có đỉnh là đỉnh của đa giác đều lại ra được như kia vậy ạ :(((

Xét tập X = {A, B, C, D, E ; F}. Với mỗi cách chọn hai phần tử của tập X và sắp xếp theo một thứ tự ta được một vectơ thỏa mãn yêu cầu
Mỗi vectơ thỏa mãn yêu cầu tương ứng cho ta một chỉnh hợp chập 2 của 6 phần tử thuộc tập X.
Vậy số các vectơ thỏa mãn yêu cầu bằng số tất cả các chỉnh hợp chập 2 của 6, bằng
Chọn C.

Áp dụng tính chất 2, ta có \(\left( P \right)\) là mặt phẳng duy nhất đi qua ba điểm phân biệt \(A,B,C\) là mặt phẳng \(M,N,O\).
Áp dụng tính chất 3, ta có
– Đường thẳng \(a\) có hai điểm phân biệt \(M,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(a\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(a\) nằm trong mặt phẳng \(\left( P \right)\).
– Đường thẳng \(b\) có hai điểm phân biệt \(N,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(b\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(b\) nằm trong mặt phẳng \(\left( P \right)\).

Chọn B
Số vectơ khác 0 ⇀ , có điểm đầu và điểm cuối lấy từ 10 điểm phân biệt trong mặt phẳng là A 10 2

Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d1 và hai đỉnh thuộc d2. Loại này có ![]() tam giác.
tam giác.
Loại 2: Tam giác có một đỉnh thuộc d2 và hai đỉnh thuộc d1. Loại này có ![]() tam giác.
tam giác.
Theo bài ra ta có: ![]()
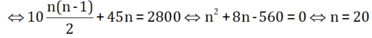
Chọn A.



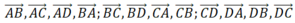
Chọn A
Hai điểm bất kì trong n điểm trên tạo thành hai véctơ thỏa mãn yêu cầu bài toán. Nên số các véc tơ đó là: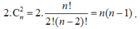
Nhận xét: Có thể hiểu mỗi véctơ là một chỉnh hợp chập 2 của n điểm. Nên số véctơ là: