Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ampe kế đo R1(theo bổ sung)=>I1=0,5A
R1//R2 \(=>Um=U1.I1=0,5.15=7,5V\)
\(=>Im=\dfrac{Um}{\dfrac{R1R2}{R1+R2}}=\dfrac{7,5}{\dfrac{15.10}{15+10}}=1,25A\)
hình đâu bạn biết là mắc song song 2 điện trở nhưng ampe kế đo cddd ở R mấy nếu đo toàn mạch thì ý b, hỏi thừa à

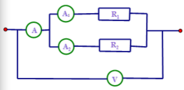
Dự đoán mạch: \(\left(R_1//R_2\right)ntR_3\)
Như vậy thì kết quả mới đẹp.
\(R_{12}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{15\cdot10}{15+10}=6\Omega\)
\(R_{tđ}=R_{12}+R_3=6+4=10\Omega\)
\(I=\dfrac{U}{R}=\dfrac{9}{10}=0,9A\)
\(U_1=I_{12}\cdot R_{12}=0,9\cdot6=5,4V\)
\(P_1=\dfrac{U_1^2}{R_1}=\dfrac{5,4^2}{15}=1,944W\)

Cường độ dòng điện qua mạch chính là:
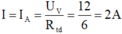
Vì R 1 mắc song song với R 2 nên U 1 = U 2 = U V = 12V
→ I 1 = U 1 / R 1 = 12/15 = 0,8A.
I 2 = U 2 / R 2 = 12/10 = 1,2A.
Vậy ampe kế ở mạch chính chỉ 2A, ampe kế 1 chỉ 0,8A, ampe kế 2 chỉ 1,2A.

a. \(R=R1+\left(\dfrac{R2.R3}{R2+R3}\right)=30+\left(\dfrac{15.10}{15+10}\right)=36\left(\Omega\right)\)
b. \(I=I1=I23=\dfrac{U}{R}=\dfrac{24}{36}=\dfrac{2}{3}A\left(R1ntR23\right)\)
\(U23=U2=U3=I23.R23=\dfrac{2}{3}\left(\dfrac{15.10}{15+10}\right)=4V\)(R2//R3)
\(\left\{{}\begin{matrix}I2=U2:R2=4:15=\dfrac{4}{15}A\\I3=U3:R3=4:10=0,4A\end{matrix}\right.\)

+ Vì hai điện trở R1 và R2 mắc song song nên U = U1 = U2
+ Vậy số chỉ của vôn kế là
U = U1 = I1R1 = 0,5.15 = 7,5V
Đáp án: A

a,\(R_{23}=\dfrac{R_2R_3}{R_2+R_3}=\dfrac{4\cdot4}{4+4}=2\left(\Omega\right)\)
\(R_{TĐ}=R_1+R_{23}=2+2=4\left(\Omega\right)\)
\(I_1=I_{23}=I=\dfrac{U_{AB}}{R_{TĐ}}=\dfrac{6}{4}=1,5\left(A\right)\)
\(U_2=U_3=U_{23}=I_{23}R_{23}=1,5\cdot2=3\left(V\right)\)
\(I_A=I_3=\dfrac{U_3}{R_3}=\dfrac{3}{4}=0,75\left(A\right)\)
R1 nt(R2//R3)
\(\Rightarrow I1=\dfrac{U}{R1+\dfrac{R2R3}{R2+R3}}=1,5A=I23\)
\(\Rightarrow U23=U3=I23R23=3V\Rightarrow Ia=I3=\dfrac{U3}{R3}=\dfrac{3}{4}A=0,75A\)
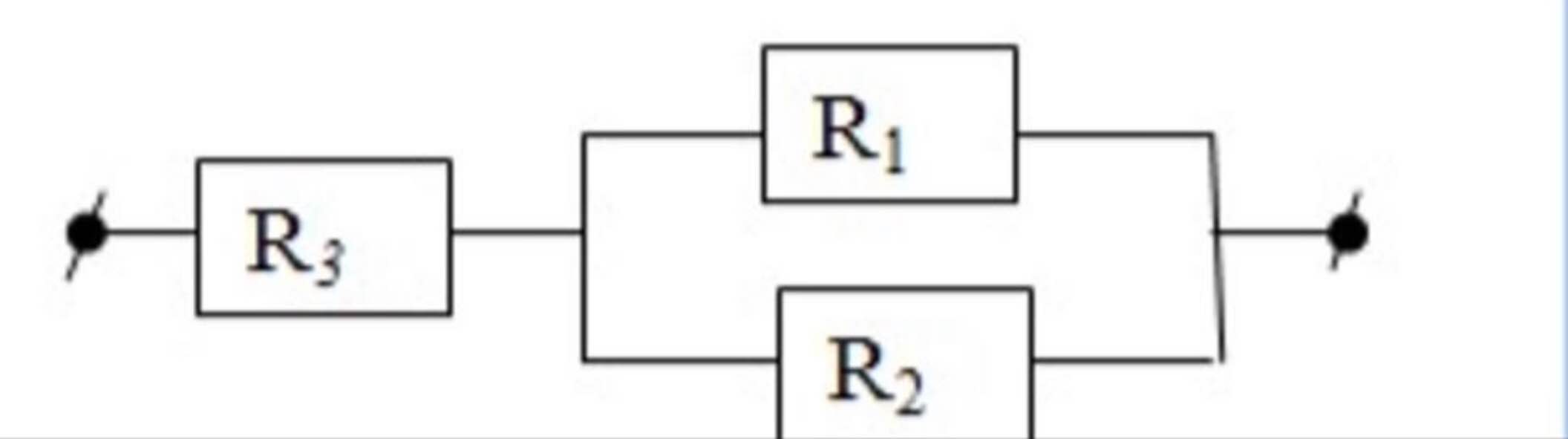
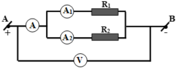
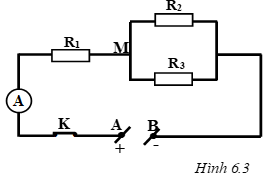

\(\dfrac{1}{R}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=\dfrac{1}{4}+\dfrac{1}{10}+\dfrac{1}{15}=\dfrac{5}{12}\Rightarrow R=2,4\left(\Omega\right)\)
\(\Rightarrow I=\dfrac{U}{R}=\dfrac{24}{2,4}=10\left(A\right)\)