Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C
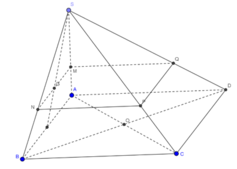
Cách 1. Ta có mặt phẳng (P) đi qua trọng tâm của tam giác SAB cắt các cạnh của khối chóp lần lượt tại M, N, P, Q. Với MN//AB, NP//BC, PQ//CD, QM//AD.
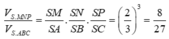
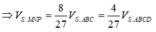
Tương tự 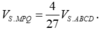
Nên 
Đặt AB = x.
Ta có 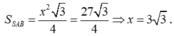
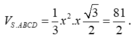
Từ đó 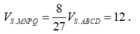
Cách 2. Do hai khối chóp S.MNPQ, S.ABCD đồng dạng với nhau theo tỉ số k = 2 3 nên tỉ lệ thể tích là
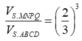
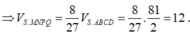

Đáp án D
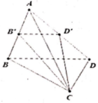
Áp dụng công thức tính tỉ số thể tích, ta có
V A . B ' C D ' V A . B C D = A B ' A B . A C A C . A D ' A D = 1 4
⇔ V A . B ' C D ' = V 4
Mà V A . B C D = V A . B ' C D ' + V C . B D D ' B '
⇒ V C . B D D ' B ' = V - V 4 = 3 V 4

Chọn B
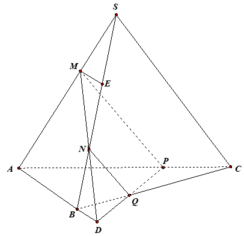
Trong mặt phẳng (SAC) dựng MP song song với SC cắt AC tại P. Trong mặt phẳng (SBC) dựng NQ song song với SC cắt BC tại Q. Gọi D là giao điểm của MN và PQ. Dựng ME song song với AB cắt SB tại E (như hình vẽ).
Ta thấy: ![]()
Suy ra N là trung điểm của BE và DM, đồng thời
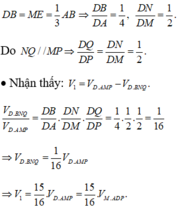
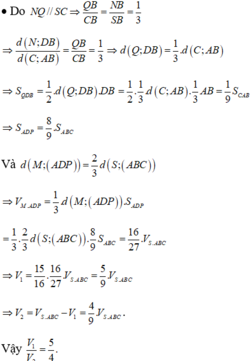

Đáp án D
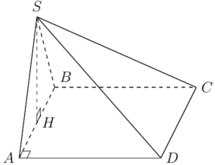
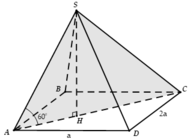
Gọi H là trung điểm AB, do tam giác SAB đều nên SA ⊥ AB. Mặt khác mặt phẳng (SAB) vuông góc với mặt đáy nên SH là đường cao của chóp.
Ta có h = S H = a 3 2 , S A B C D = a 2
Vậy V = 1 3 . a 3 2 . a 2 = a 3 3 6
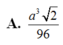
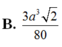
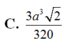
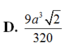

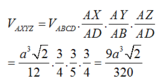
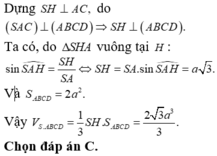
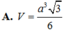
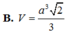
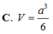
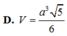


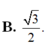
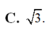
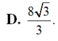
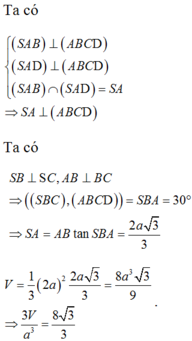

Chọn C
Gọi G₁, G₂, G₃ lần lượt là trọng tâm các tam giác SAB, SAD, SAC.
Gọi I, J lần lượt là trung điểm của AB, AC thì
Qua G₁ dựng đường song song với AB, cắt SA, SB lần lượt tại M, N.
Qua N dựng đường song song với BC, cắt SC tại P.
Qua P dựng đường song song với CD, cắt SD tại Q.
=> Thiết diện của hình chóp S. ABCD khi cắt bới (G₁G₂G₃) là tứ giác MNPQ.