Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp:
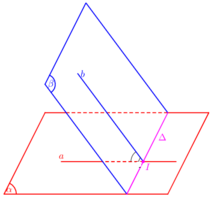
Xác định góc giữa hai mặt phẳng (α;β)
- Tìm giao tuyến Δ của (α;β)
- Xác định 1 mặt phẳng γ ⊥ Δ
- Tìm các giao tuyến a = α∩γ, b = β ∩ γ
- Góc giữa hai mặt phẳng (α;β):(α;β) = (a;b)
Cách giải:
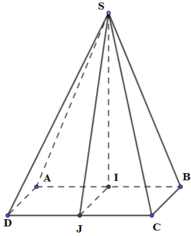
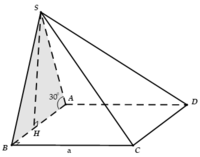
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB cân tại S ⇒ SI ⊥ AB
Vì mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD) nên SI ⊥ (ABCD)
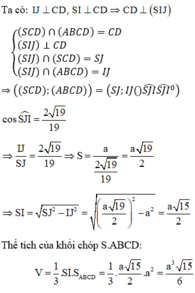

Chọn D.
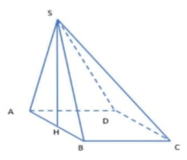
Ta có: SA=SB=AB=a 3
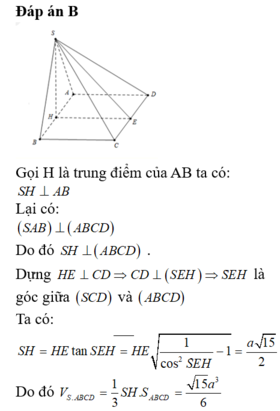
Gọi H là trung điểm của AB.
Do (SAB) ⊥ (ABCD) nên SH ⊥ (ABCD). Khi đó SH= 3 a 2
Diện tích đáy S A B C D = 3 a 2
Vậy thể tích khối chóp
V
S
.
A
B
C
D
=
1
3
S
H
.
S
A
B
C
D
=
3
a
2
2

Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
\(SH=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{1}{3}SH.AB^2=\dfrac{1}{3}.\dfrac{a\sqrt{6}}{2}.2a^2=\dfrac{a^3\sqrt{6}}{3}\)
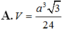
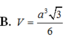
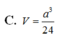
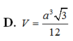
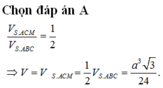
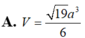
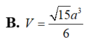
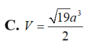
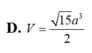
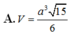
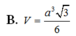
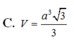
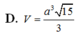




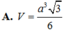
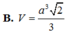
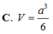
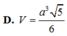

Đáp án D
Gọi H là trung điểm AB, do tam giác SAB đều nên SA ⊥ AB. Mặt khác mặt phẳng (SAB) vuông góc với mặt đáy nên SH là đường cao của chóp.
Ta có h = S H = a 3 2 , S A B C D = a 2
Vậy V = 1 3 . a 3 2 . a 2 = a 3 3 6