Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

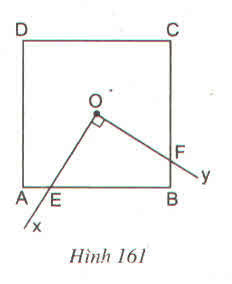
Nối OA, OB.
Xét \(\Delta\)AOE và \(\Delta\)BOF có:
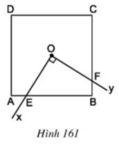
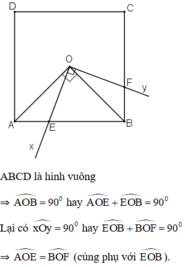
+ \(\widehat{AOE}=\widehat{BOF}\) (cùng phụ với \(\widehat{BOE}\))
+ OA = OB (O là tâm đối xứng)
+ \(\widehat{OAE}=\widehat{OBE}=45^o\)
=> ∆AOE = ∆BOF (g - c - g)
Do đó: \(S_{OEBF}=S_{OEB}+S_{OBF}=S_{OEB}+S_{OAE}=S_{OAE}+S_{OEB}=S_{OAB}\)
Vậy \(S_{OEBF}=\dfrac{1}{4}S_{ABCD}\)
Nối OA, OB.
Xét ΔAOE và ΔBOF có:
+) \(\widehat{AOE}=\widehat{BOF}\) ( cùng phụ với BOE )
+) OA = OB ( O là tâm đối xứng )
+) \(\widehat{OAE}=\widehat{OBF}=45^0\)
⇒ ΔAOE = ΔBOF.
⇒ \(S_{OEBF}=S_{OEB}+S_{OBF}=S_{OEB}+S_{OAE}=S_{OAE}+S_{OAB}\)
⇒ \(S_{OEBF}=\frac{1}{4}S_{ABCD}.\)

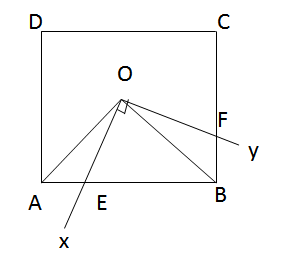
từ O hạ đường cao OH,OK ứng với AB và BC => OH=OK=8cm
có tgAOE=tgBOF (g.c.g) do
góc AOE=góc BOF (cùng phụ với xOy)
OA=OB
góc BOA= góc ABO (cùng phụ với góc ABO)
=> AE=BF
SOEBF = SEOB + SBOF = OH.EB/2 + OK.BF/2= OH( EB/2 + BF/2)= OH.((EB+AE)/2 )=(8.16)/2=64 cm2
SOEBF= SEOB + SBOF =

Bài 2 :
D C A B H O E F G x y
Các tia đối Ox,Oy cắt CD, DAtheo thứ tự G, H
Do t/c đối xứng nên diện tích tứ giác OEBF = dt tứ giác OFCG = dt tứ giác OGDH= dt tứ giác OHAE
Mà tổng diện tích 4 tứ giác đó = dt hình vuông ABCD = a2
=> Diện tích tứ giác OEBF = \(\frac{a^2}{4}\)

https://hoc24.vn/hoi-dap/question/18469.html
tham khảo đi bạn
giống đó

Nối OA,OBOA,OB. Hai tam giác AOEAOE và BOFBOF có:
ˆAOE=ˆBOFAOE^=BOF^ (cùng phụ với ˆBOEBOE^)
OA=OBOA=OB (O là tâm đối xứng của hình vuông)
ˆOAE=ˆOBF=450OAE^=OBF^=450 (tính chất hình vuông)
Nên ΔAOE=ΔBOF(g−c−c)
Do đó
SOBEF=SOEB+SOBF=SOEB+SOAE=SOAB
Vậy SOEFB=\(\dfrac{1}{2}\)SABCD=\(\dfrac{1}{4}\)a2