Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Độ dài đường chéo là \(5\sqrt{2}\left(cm\right)\)
Diện tích của hình thoi là: 6 .8 : 2 = 24 cm^2
Cạnh của hình thoi là: \(\sqrt{\left(\frac{6}{2}\right)^2+\left(\frac{8}{2}\right)^2}=5\) cm
Chiều cao của hình thoi là: 24 : 5 = 4,8 cm
Vậy:...
Độ dài đường chéo của hình thoi lần lượt là
→ Độ dài đường chéo của hình thoi là:
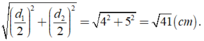
Chọn đáp án B.
DBDC, viết các cặp góc tương ứng bằng nhau của hai tam giác đã cho. 
có AB = 3cm, AC = 4,5cm, BC = 6cm. 
có DE= 12cm, EF=9cm, DF = 6cm. Chứng minh 
. 
AC). Tính AN? 
nhọn. Trên cạnh Ox, đặt các đoạn thẳng OA = 6cm, OB = 18cm. Trên cạnh Oy, đặt các đoạn thẳng OC = 9cm, OD = 12cm.Chứng minh hai tam giác OAD và OCB đồng dạng. 
có 
và 
có MN = 6cm; MP = 8cm; 
đồng dạng với 
Câu 11:
Xét ΔABC và ΔMNP có
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}\left(=\dfrac{1}{2}\right)\)
Do đó: ΔABC~ΔMNP
Câu 12:
a: Xét ΔAMC và ΔANB có
\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\left(\dfrac{10}{8}=\dfrac{15}{12}\right)\)
\(\widehat{MAC}\) chung
Do đó: ΔAMC đồng dạng với ΔANB
b: Ta có: ΔAMC đồng dạng với ΔANB
=>\(\widehat{ACM}=\widehat{ABN}\)
Xét ΔHMB và ΔHNC có
\(\widehat{HBM}=\widehat{HCN}\)
\(\widehat{MHB}=\widehat{NHC}\)(hai góc đối đỉnh)
Do đó; ΔHMB đồng dạng với ΔHNC
=>\(\dfrac{HB}{HC}=\dfrac{BM}{CN}\)
=>\(HB\cdot CN=BM\cdot CH\)
Câu 10:
Xét ΔOAD và ΔOCB có
\(\dfrac{OA}{OC}=\dfrac{OD}{OB}\)
góc O chung
Do đó: ΔOAD~ΔOCB
Ta có :
( 10 : 2 )2 + ( 6 : 2 )2 = x2 ( Theo định lí Py-ta-go )
=> 52 + 32 = x2
=> 25 + 9 = x2
=> 34 = x2
=> \(\sqrt{34}=x\)
Vậy cạnh hình thoi có độ dài = \(\sqrt{34}\).
vẽ là hthoi ABCD, O là Giao điểm 2 đường chéo nha
Ta có AC=8=> OA=4
DB=6=>OD=3
=> AD=\(\sqrt{OA^2+OD^2}=\sqrt{4^2+3^2}=5\)