Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
Gọi mỗi đinh của tứ giác là A, B, C, D. Các góc ngoài tương ứng lần lượt là A1, B1, C1, D1
Ta có: A+ B+ C+ D+ A1+ B1+ C1+ D1= 720 độ
Ma A+ B+ C+ D= 360 độ nên A1+ B1+ C1+ D1= 720 - 360= 360 độ

\(\text{#3107}\)
1.
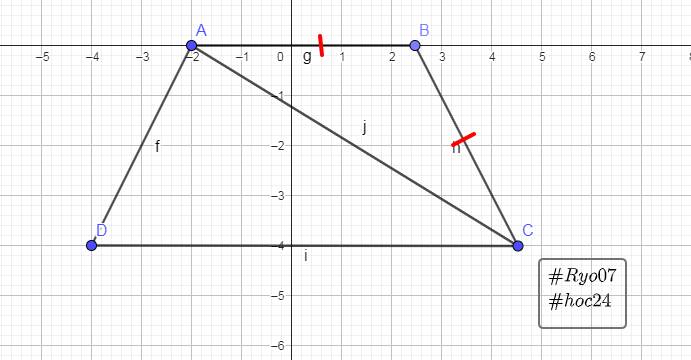
Ta có: \(\text{AB // CD}\)
\(\Rightarrow\widehat{\text{BAC}}=\widehat{\text{ACD}}\left(\text{2 góc sole trong}\right)\) `(1)`
Xét `\Delta ABC:`
\(\text{AB = BC (gt)}\)
\(\Rightarrow\) `\Delta ABC` cân tại B
\(\Rightarrow\widehat{\text{BAC}}=\widehat{\text{BCA}}\) `(2)`
Từ `(1)` và `(2)`
\(\Rightarrow\widehat{\text{ACB}}=\widehat{\text{ACD}}\)
Mà \(\widehat{\text{ACB}}+\widehat{\text{ACD}}=\widehat{\text{BCD}}\)
\(\Rightarrow\) CA là phân giác của \(\widehat{\text{BCD}}.\)
Xét tứ giác ABCD có
AB=BC=CD=AD
nên ABCD là hình thoi
Suy ra: \(\widehat{A}=\widehat{C}\)
mà \(\widehat{A}=\widehat{B}\)
nên \(\widehat{B}=\widehat{C}=90^0\)
\(\Leftrightarrow\widehat{A}=\widehat{D}=90^0\)