Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

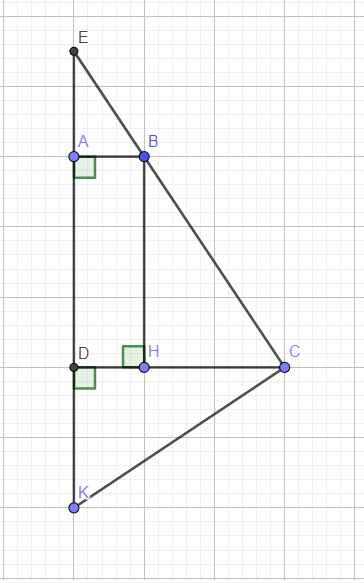
Do \(AD\perp CD\Rightarrow\) hình thang ABCD vuông tại A và D
\(\Rightarrow\) Tứ giác ABHD là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AD=BH\) \(\Rightarrow BH=CD\)
Xét hai tam giác vuông BCH và CKD có:
\(\left\{{}\begin{matrix}BH=CD\\DK=CH\end{matrix}\right.\) \(\Rightarrow\Delta BCH=\Delta CKD\left(c.g.c\right)\) (1)
\(\Rightarrow\widehat{DCK}=\widehat{HBC}\)
\(\Rightarrow\widehat{BCK}=\widehat{BCH}+\widehat{DCK}=\widehat{BCH}+\widehat{HBC}=90^0\)
\(\Rightarrow BC\perp CK\)
b. Cũng từ (1) ta suy ra \(CB=CK\)
Áp dụng hệ thức lượng trong tam giác vuông ECK với đường cao CD:
\(\dfrac{1}{CD^2}=\dfrac{1}{CE^2}+\dfrac{1}{CK^2}=\dfrac{1}{CE^2}+\dfrac{1}{CB^2}\) (đpcm)

bài này ko khó nếu nắm rõ công thức
A)Ta có AD=DC ( giả thiết )
mà AD=BH ( cùng là chiều cao của hình thang)
=>BH=DC
=>Tam giác Dkc=Tam giác HCB (cạnh huyền cạnh góc vuông)
=>góc DKC=góc HCB (hai góc tương ứng )
mà Góc DKC+ góc DCK = 90 độ
=>góc HCB+ góc DCk=90
=>góc BCK=90 độ=> BC vuông góc với Ck
B )Tam giác ECK vuông tại C ( do câu a)
=>1/CD^2=1/EC^2+1/Ck^2
mà
Tam giác Dkc=Tam giác HCB (cạnh huyền cạnh góc vuông)
=> CK=CB
=>
1/CD^2=1/EC^2+1/CB^2

Để giải bài toán này, chúng ta có thể sử dụng định lí Euclid và các quy tắc về góc và đường thẳng. Hãy xem xét từng câu hỏi một.
a) Để tính AC, ta có thể sử dụng định lí Pythagoras trong tam giác ABC. Với AB = 4cm và BC = 3cm, ta có AC = √(AB^2 + BC^2). Tương tự, để tính AH và BH, ta có AH = AB và BH = BC.
b) Để chứng minh rằng BH.BE = CH.AC, ta có thể sử dụng các quy tắc về tỉ lệ đồng dạng của tam giác. Bằng cách chứng minh rằng tam giác AHB và tam giác CHB đồng dạng, ta có thể suy ra công thức trên.
c) Để chứng minh góc ADH = góc ACK, ta có thể sử dụng các quy tắc về góc đồng quy và góc nội tiếp. Bằng cách chứng minh rằng góc ADH và góc ACK đồng quy với góc nội tiếp tại cùng một cung, ta có thể suy ra bằng chứng cần thiết