Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔDAB có OI//AB
nên \(\dfrac{OI}{AB}=\dfrac{DO}{DB}\)
Xét ΔBDC có OK//DC
nên \(\dfrac{OK}{CD}=\dfrac{BO}{BD}\)
=>\(\dfrac{OI}{AB}+\dfrac{OK}{CD}=\dfrac{BO}{BD}+\dfrac{DO}{DB}=1\)
Xét ΔADC có OI//DC
nên \(\dfrac{OI}{DC}=\dfrac{AI}{AD}\)
Xét ΔBDC có OK//DC
nên \(\dfrac{OK}{DC}=\dfrac{BK}{BC}\)
Xét hình thang ABCD có IK//AB//CD
nên \(\dfrac{AI}{AD}=\dfrac{BK}{BC}\)
=>\(\dfrac{OI}{DC}=\dfrac{OK}{DC}\)
=>OI=OK
=>\(\dfrac{OI}{AB}+\dfrac{OK}{CD}=\dfrac{OI}{AB}+\dfrac{OI}{CD}=1\)

a, xét tam giác ODC có : AB // DC
=> OA/OC = OB/OD = AB/DC (đl)
có : AB = 4; DC = 9 (gt)
=> OA/OC = OB/OD = 4/9
B, xét tam giác ABD có : EO // AB (gt) => EO/AB = DO/DB (hệ quả) (1)
xét tam giác ABC có FO // AB (gt) => OF/AB = CO/CA (hệ quả) (2)
xét tam giác ODC có AB // DC (gt) => DO/DB = CO/CA (hệ quả) (3)
(1)(2)(3) => OE/AB = OF/AB
=> OE = OF
xét tam giác ABD có : EO // AB(Gt) => EO/AB = DE/AD (hệ quả) (4)
xét tam giác ADC có EO // DC (gt) => OE/DC = EA/AD (hệ quả) (5)
(4)(5) => EO/AB + EO/DC = DE/AD + AE/AD
=> EO(1/AB + 1/DC) = 1 (*)
xét tam giác ACB có FO // AB (gt) => OF/AB = FC/BC (hệ quả) (6)
xét tam giác BDC có OF // DC (gt) => OF/DC = BF/BC (hệ quả) (7)
(6)(7) => OF/AB + OF/DC = FC/BC + BF/BC
=> OF(1/AB + 1/DC) = 1 (**)
(*)(**) => OF(1/AB + 1/DC) + OE(1/AB + 1/DC) = 1 + 1
=> (OE + OF)(1/AB + 1/DC) = 2
=> EF(1/AB + 1/DC) = 2
=> 1/AB + 1/DC = 2/EF
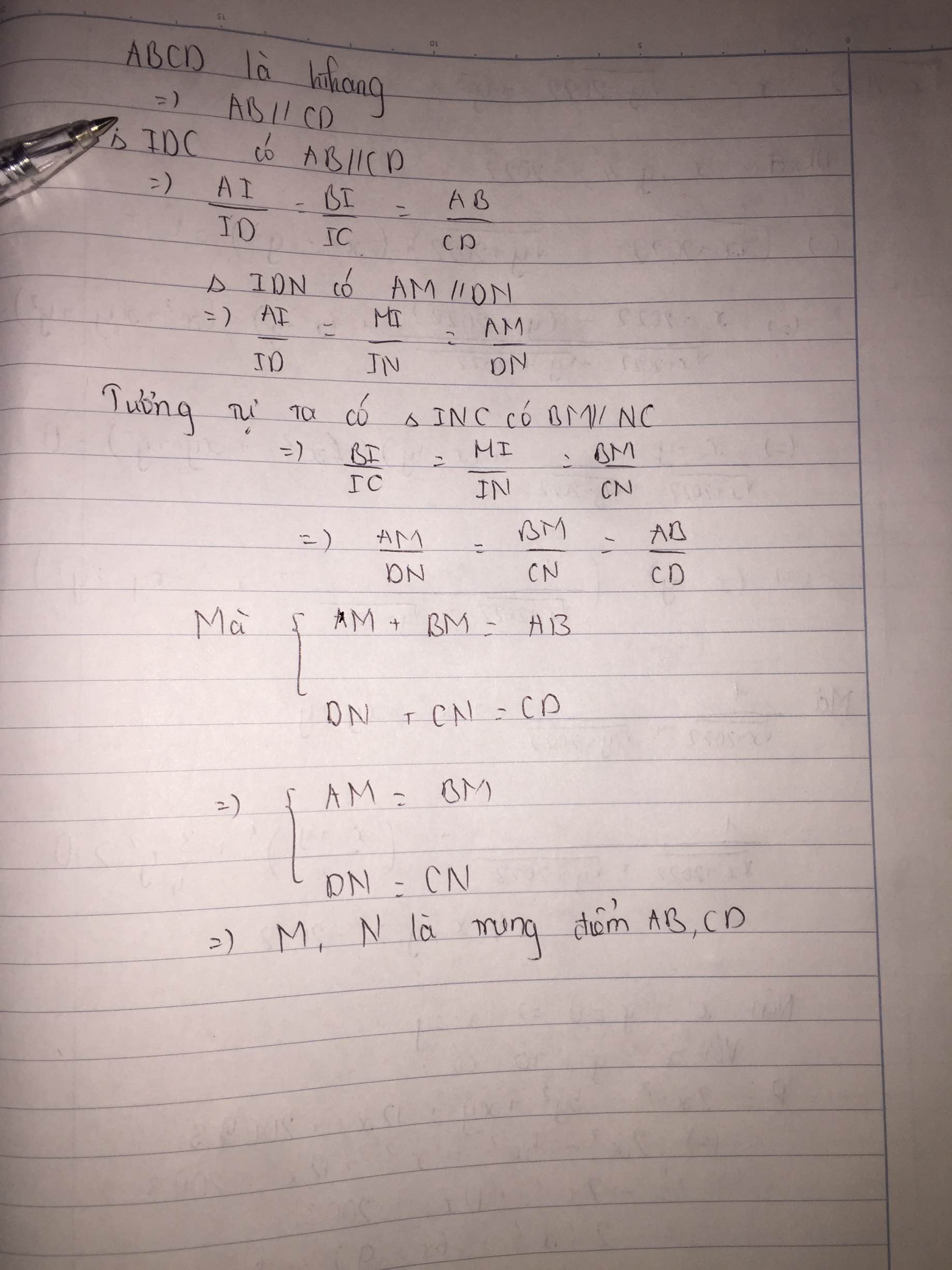
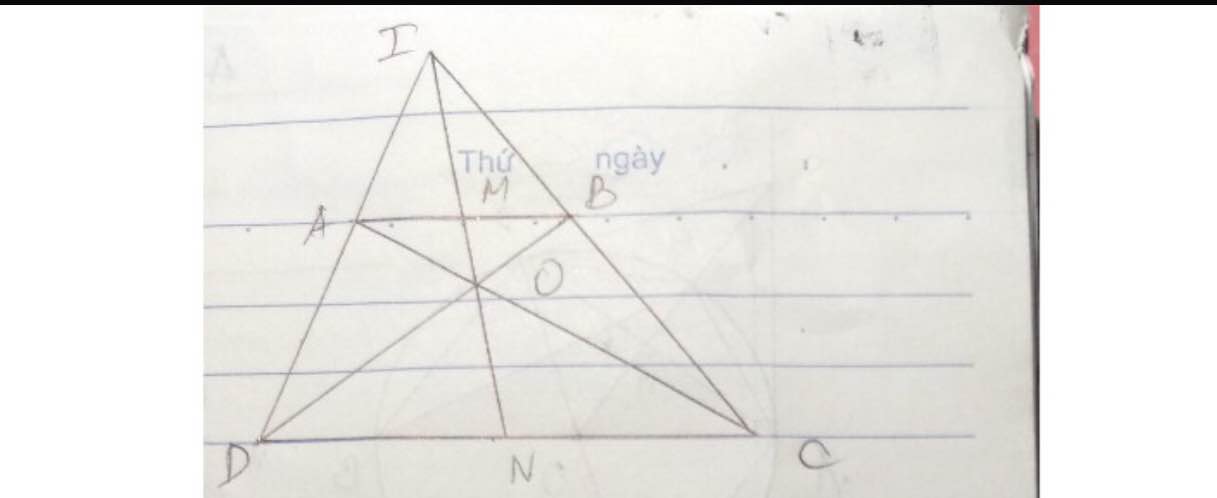
a. Xét △BDC có: OI//DC (gt).
=>\(\dfrac{OI}{DC}=\dfrac{BO}{BD}\) (định lí Ta-let).
=>\(\dfrac{DC}{OI}=\dfrac{BD}{BO}\)
=>\(\dfrac{DC}{OI}-1=\dfrac{OD}{BO}\)
-Xét △ABO có: AB//DC (gt).
=>\(\dfrac{OD}{BO}=\dfrac{DC}{AB}\) (định lí Ta-let).
Mà \(\dfrac{DC}{OI}-1=\dfrac{OD}{BO}\) (cmt).
=>\(\dfrac{DC}{OI}-1=\dfrac{DC}{AB}\)
=>\(\dfrac{DC}{OI}=\dfrac{DC}{AB}+1=\dfrac{AB+DC}{AB}\)
=>\(\dfrac{1}{OI}=\dfrac{AB+DC}{AB.DC}=\dfrac{1}{AB}+\dfrac{1}{DC}\).