Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

THAM KHẢO:

a) Vì AA′⊥(ABCD) nên góc giữa đường thẳng AA' và (ABCD) là \(90^0\)
b) CC′⊥(ABCD) nên C là hình chiếu vuông góc của C' lên (ABCD).
Suy ra góc giữa BC' và (ABCD) là \(\widehat{C'BC}\)=\(45^O\) (Vì BCC'C' là hình vuông)c) Gọi cạnh của hình lập phương là a
Ta có: AC=\(a\sqrt{2}\),tan \(\widehat{ACA'}\)=\(\dfrac{1}{\sqrt{2}}\) nên \(\widehat{ACA'}\)=\(35^O\)
AA′⊥(ABCD) nên A là hình chiếu vuông góc của A' lên (ABCD)
Suy ra góc giữa A'C và (ABCD) là \(\widehat{ACA'}\)=\(35^O\)

a: ABCD.A'B'C'D' là hình lập phương
=>AA'//BB'//CC'//DD' và AA'=BB'=CC'=DD'
Xét tứ giác AA'C'C có
AA'//CC'
AA'=CC'
Do đó: AA'C'C là hình bình hành
=>AC//A'C'
ABCD.A'B'C'D' là hình lập phương
=>ABCD và A'B'C'D' là hình vuông
ABCD là hình vuông
=>AC là phân giác của góc BAD và CA là phân giác của góc BCD
=>\(\widehat{BAC}=\widehat{DAC}=45^0\) và \(\widehat{BCA}=\widehat{DCA}=45^0\)
\(\widehat{A'C';BC}=\widehat{AC;BC}=\widehat{ACB}=45^0\)
b: Xét ΔBAC có M,N lần lượt là trung điểm của BC,BA
=>MN là đường trung bình của ΔBAC
=>MN//AC
Xét ΔA'AD' có
E,F lần lượt là trung điểm của AA',A'D'
=>EF là đường trung bình của ΔA'AD'
=>EF//AD'
ABCD.A'B'C'D là hình vuông
=>ADD'A' là hình vuông; DCC'D' là hình vuông
ABCD là hình vuông
=>\(AC=AB\cdot\sqrt{2}\)(1)
ADD'A' là hình vuông
=>\(AD'=AD\cdot\sqrt{2}=AB\cdot\sqrt{2}\)(2)
DCC'D' là hình vuông
=>\(CD'=CD\cdot\sqrt{2}=AB\cdot\sqrt{2}\left(3\right)\)
Từ (1),(2),(3) suy ra AC=AD'=D'C
=>ΔAD'C đều
=>\(\widehat{D'AC}=60^0\)
\(\widehat{MN;EF}=\widehat{AC;AD'}=\widehat{CAD'}=60^0\)
c: \(\widehat{MN;BC}=\widehat{AC;CB}=\widehat{ACB}=45^0\)
d: \(\widehat{EF;CC'}=\widehat{AD';DD'}=\widehat{AD'D}=45^0\)

Đáp án B
Gọi M là trung điểm C’D’. Đặt x là cạnh của hình lập phương
Ta có
![]()
![]()
![]()
Gọi O là trung điểm A’C. Dễ dàng chứng minh OM ⊥ (A'B'CD) (xin dành cho bạn đọc).
Suy ra
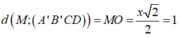
![]()
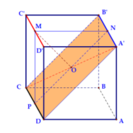

Đáp án D
Có hình chiếu của AC' xuống đáy là AC mà AC ⊥ BC nên AC'BD.

Đáp án A.
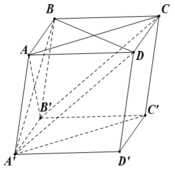
Ta có AA'BC là chóp đều có tất cả các cạnh bằng 1
![]()
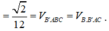
Ta có ![]()
![]()
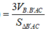
Lại có
∆
AB'C có B'C = A'D = 1; ![]() (do là hình thoi cạnh 1 có
B
A
D
^
=
60
0
)
(do là hình thoi cạnh 1 có
B
A
D
^
=
60
0
)
Do đó
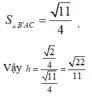

\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
Ý A
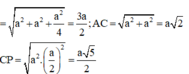
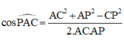
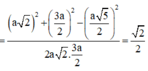
Do \(AC||A'C'\Rightarrow\widehat{\left(AD;A'C'\right)}=\widehat{\left(AD;AC\right)}=\widehat{CAD}=45^0\)