Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(BCC'B'\) là hình chữ nhật \( \Rightarrow BC\parallel B'C'\)
\( \Rightarrow \left( {AB,B'C'} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^ \circ }\).
b)
\(\Delta AA'B\) vuông tại \(A \Rightarrow \tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {ABA'} = {45^ \circ }\)
Vậy \(\left( {A'B,\left( {ABC} \right)} \right) = {45^ \circ }\).
c) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot BC,CC' \bot CM\)
Vậy \(\widehat {BCM}\) là góc nhị diện \(\left[ {B,CC',M} \right]\).
\(\Delta ABC\) đều \( \Rightarrow \widehat {BCM} = \frac{1}{2}\widehat {ACB} = {30^ \circ }\).
d) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right)\)
\(\Delta ABC\) đều \( \Rightarrow CM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).
\(\left. \begin{array}{l}CC'\parallel AA'\\AA' \subset \left( {ABB'A'} \right)\end{array} \right\} \Rightarrow CC'\parallel \left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC',\left( {ABB'A'} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right) \Rightarrow CM \bot A'M\)
\(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot CM\)
\( \Rightarrow d\left( {CC',A'M} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
g) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4},h = AA' = a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{4}\)
\({S_{\Delta MBC}} = \frac{1}{2}{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{8},h = AA' = a\)
\( \Rightarrow {V_{A'.MBC}} = \frac{1}{3}{S_{\Delta MBC}}.AA' = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{8}.a = \frac{{{a^3}\sqrt 3 }}{{24}}\)
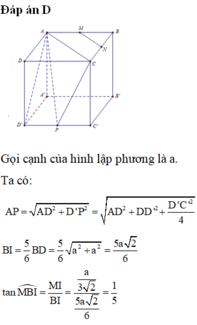
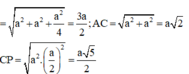
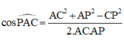
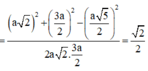
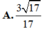

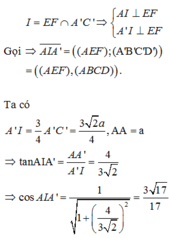
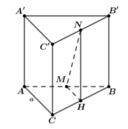
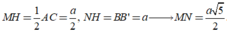
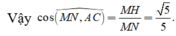

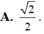
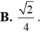
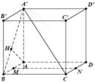
\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
Ý A
Chọn A