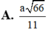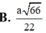Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
là trọng tâm tam giác SAE.
Tứ diện AEND vuông tại đỉnh A nên
Vậy

Đáp án C
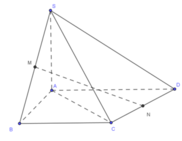
Kẻ CN
⊥
AB ta dễ dàng tính được ![]()
![]()
=> tam giác ADC vuông tại C. Từ đó NC ⊥ (SAC)
Gọi O là trung điểm của AC, dễ dàng cm được BD ⊥ (SAC)
=> MK ⊥ (SAC). vơí K là trung điểm của SO, từ đó KC là hc của MN lên .
Ta kẻ KZ ⊥ AC
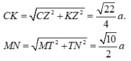
với T là trung điểm của AB.
Gọi α là góc tạo với MN và (SAC)
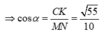

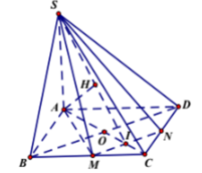
Gọi I = AC ∩ MN ⇒ I là trung điểm của OC, ta có:
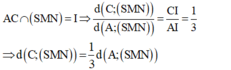
- Ta có: MN// BD mà BD ⊥ (SAC)(cmt) ⇒ MN ⊥ (SAC).
- Trong (SAC) kẻ AH ⊥ SI (H ∈ SI) ⇒ MN ⊥ AH.
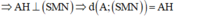
- Ta có:
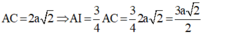
- Xét tam giác vuông SAI ta có:
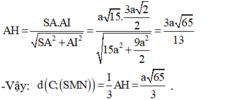

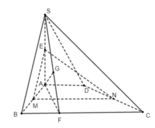
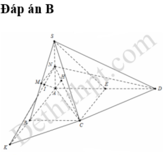
+ Ta có: M N // B C ⇒ M N // S B C E M // S B ⇒ E M // S B C ⇒ M N E // S B C
⇒ d((MNE); (SBC)) = d(M; (SBC))
+ Lại có: AM ∩ (SBC) = B ⇒ d A ; S B C d M ; S B C = A B M B = 2 ⇒ d(M; (SBC)) = 1/2 d(A;(SBC))
⇒ d ((MNE);(SBC)) = 1/2 d(A;(SBC))
+ Từ A hạ AF ⊥ BC tại F, AG ⊥ SF tại G
B C ⊥ S A B C ⊥ A F ⇒ B C ⊥ S A F ⇒ B C ⊥ A G mà AG ⊥ SF nên AG ⊥ (SBC)
⇒ d(A;(SBC)) = AG
+ Tính AG
Do ABCD là hình thang cân, BC = 2a nên suy ra BF = a/2
⇒ AF = BF. tan 60 ° = a 3 2
Tam giác SAF vuông tại A có AG là đường cao
⇒ 1 A G 2 = 1 S A 2 + 1 A F 2 ⇒ AG = a 66 11
⇒ d ((MNE);(SBC)) = 1/2 d(A;(SBC)) = 1/2 AG = a 66 22 .
Đáp án C

Đáp án B
Gọi H 1 là chân đường cao kẻ từ H đến DC. H 2 là chân đường cao kẻ từ H đến S H 1 . Khi đó ta có
![]()
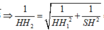
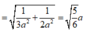
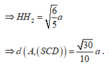
=> Chọn phương án B.