

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




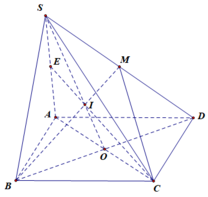
Trong mp(ABCD), gọi \(O=AC\cap BD\)
a) Ta có:
\(\left\{{}\begin{matrix}S\in\left(SAC\right)\\S\in\left(SBD\right)\end{matrix}\right.\)\(\Rightarrow S\in\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}O\in BD\subset\left(SBD\right)\\O\in AC\subset\left(SAC\right)\end{matrix}\right.\)\(\Rightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Trong mp(SBD), gọi \(I=SO\cap BM\Rightarrow I=BM\cap\left(SAC\right)\)
Ta có: \(\left\{{}\begin{matrix}SM=DM\\OB=OD\end{matrix}\right.\)\(\Rightarrow\dfrac{IB}{IM}=2\)
b) Ta có:
\(\left\{{}\begin{matrix}I\in SO\subset\left(SAC\right)\\I\in BM\subset\left(MBC\right)\end{matrix}\right.\)\(\Rightarrow I\in\left(SAC\right)\cap\left(MBC\right)\)
\(\left\{{}\begin{matrix}C\in\left(SAC\right)\\C\in\left(MBC\right)\end{matrix}\right.\)\(\Rightarrow C\in\left(SAC\right)\cap\left(MBC\right)\)
\(\Rightarrow IC=\left(SAC\right)\cap\left(MBC\right)\)
Trong mp(SAC), gọi \(J=SA\cap IC\)\(\Rightarrow J=SA\cap\left(MBC\right)\)
Theo định lý Menelaus, ta có:
\(\dfrac{JS}{JA}.\dfrac{CA}{CO}.\dfrac{IO}{SO}=1\)\(\Rightarrow\dfrac{JS}{JA}.2.\dfrac{1}{3}=1\Leftrightarrow\dfrac{JS}{JA}=\dfrac{3}{2}\)

a: Chọn mp(SBD) có chứa BM
\(O\in BD\subset\left(SBD\right);O\in AC\subset\left(SAC\right)\)
Do đó: \(O\in\left(SBD\right)\cap\left(SAC\right)\)
mà \(S\in\left(SBD\right)\cap\left(SAC\right)\)
nên \(\left(SBD\right)\cap\left(SAC\right)=SO\)
Gọi E là giao điểm của SO với BM
=>E là giao điểm của BM với mp(SAC)
b: \(M\in SD\subset\left(SAD\right);M\in\left(MAC\right)\)
=>\(M\in\left(SAD\right)\cap\left(MAC\right)\)
mà \(A\in\left(MAC\right)\cap\left(SAD\right)\)
nên \(\left(MAC\right)\cap\left(SAD\right)=AM\)

a) Do MN\(\subset\) (BMN); AD \(\subset\)(ABCD) nên I là một điểm chung của (BMN) với (ABCD). Dễ thấy B là một điểm chung khác I
Vậy (BMN)\(\cap\) (ABCD) =BI
b) J\(\in\)BI\(\subset\) (BMN)
J \(\in\) (CD) \(\subset\) (SCD)
nên J là một điểm chung của (BMN) \(\cap\) (SCD)
vậy (SCD) \(\cap\) (BMN) =NJ
Thiết diện của (BMN) với hình chóp là tứ giác AMNJ
c) Áp dụng định lí Menelaus Trong \(\Delta SAD\) có cát tuyến MNI có:
\(\dfrac{ID}{IA}.\dfrac{MA}{MS}.\dfrac{NS}{ND}=1\)
\(\dfrac{ID}{IA}.1.2=1\) => \(\dfrac{ID}{IA}=\dfrac{1}{2}\)
=> D là trung điểm AI
+ Xét tam giác SAI có 2 trung tuyến MI, SD giao nhau tại N => N là trong tâm tam giác SAI
=> \(\dfrac{NI}{MI}=\dfrac{2}{3}\)
Ta có AD//BC
=> \(\dfrac{IK}{BK}=\dfrac{AI}{BC}=\dfrac{2AD}{BC}=2\)(do AD=BC)
=> \(\dfrac{IK}{IB}=\dfrac{2}{3}\)
Xét tam giác MIB có: \(\dfrac{NI}{MI}=\dfrac{IK}{IB}=\dfrac{2}{3}\)
=> BM//NK