Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong mp(SAD) kẻ DF//SA
SA⊥AD => DF⊥AD mà AD⊥DC => AD⊥(DCF)
Kẻ CH⊥DF => CH⊥AD => CH⊥(SAD)
=> H là hình chiếu của C lên (SAD)
=> \(\widehat{\left(SC,\left(SAD\right)\right)}=\widehat{\left(SC,SH\right)}=\widehat{CSH}\)
ΔCFD=ΔSAB => ΔCFD đều cạnh a => CH= \(\dfrac{\sqrt{3}}{2}a\)
SC= \(\sqrt{2}a\)
Xét tam giác SCH vuông ở H ta có:
sin CSH= \(\dfrac{HC}{SC}\)=\(\dfrac{\sqrt{6}}{4}\)
=> \(\widehat{CSH}\)= arcsin\(\dfrac{\sqrt{6}}{4}\)

Bạn kiểm tra lại đề,
1. ABCD là hình thang vuông tại A và B hay A và D? Theo dữ liệu này thì ko thể vuông tại B được (cạnh huyền DC nhỏ hơn cạnh góc vuông AB là cực kì vô lý)
2. SC và AC cắt nhau tại C nên giữa chúng không có khoảng cách. (khoảng cách bằng 0)
Nguyễn Việt Lâm
e xin loi a
ABCD là hình thang vuông tại A và D
còn đoạn sau khoảng cách giữa 2 đt SC và AC thì e kh biet no sai o đau
anh giup em vs ah

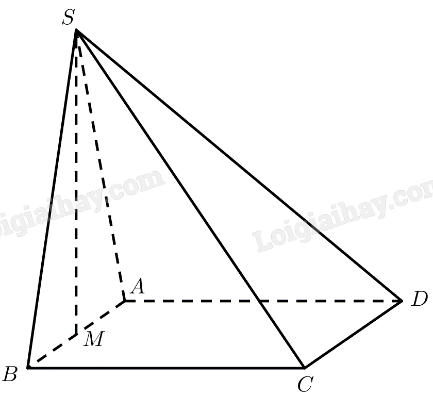
a, Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)

\(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\\left(SAB\right)\cap\left(ABCD\right)=AB\\SA\perp AB\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\widehat{SBA}=45^0\) (do SAB vuông cân tại A)
b.
\(\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=AB\sqrt{2}=2a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{SC}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SCA}\approx35^015'\)

Đề bài thiếu chi tiết định dạng điểm S nên không giải được (ví dụ phải thêm SA vuông góc mặt đáy hoặc gì đó tương tự)

a: BC vuông góc AB; BC vuông góc SA
=>BC vuông góc (SAB)
b: (BS;(BACD))=(BS;BA)=góc SBA
tan SBA=SA/AB=căn 5/2
=>góc SBA=48 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1
=>góc SCA=45 độ



a: (SAB) vuông góc (ABCD)
(SAB) giao (ABCD)=AB
SI vuông góc AB
=>SI vuông góc (ABCD)
b: CD vuông góc SI
CD vuông góc IK
=>CD vuông góc (SIK)
=>(SCD) vuông góc (SIK)