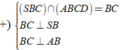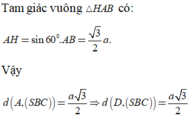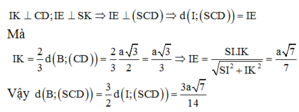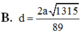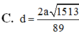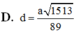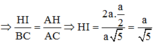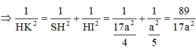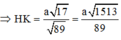Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

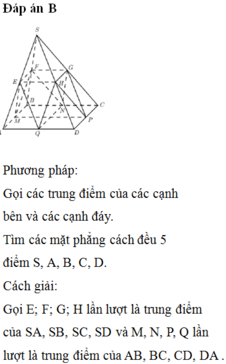
Có 5 mặt phẳng cách đều 5 điểm S, A, B, C, D:
Mặt phẳng đi qua 4 trung điểm của 4 cạnh bên: có 1 mặt.
Mặt phẳng đi qua tâm O và song song với từng mặt bên : có 4 mặt như vậy

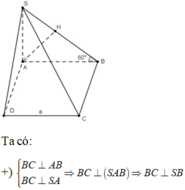
1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.
2) Ta có tam giác SAB đều nên SA =a3√2
suy ra V=13SABCD.SH=a33√6

Phương pháp:
Xác định chiều cao hình chóp bằng kiến thức 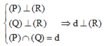
Xác định khoảng cách ![]()
Tính toán bằng cách sử dụng quan hệ diện tích, định lý hàm số cosin, công thức tính diện tích tam giác S =
1
2
a.h với a là cạnh đáy, h là chiều cao tương ứng và ![]()
Cách giải:
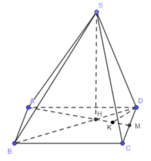
Gọi H = AM ∪ BD
Ta có 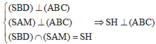
Vì AB//CD nên theo định lý Ta-lét ta có

Ta có ![]()
![]()
![]()
Vì M là trung điểm của DC và ABCD là hình bình hành có diện tích 2 a 2 nên ta có:
![]()
Lại có CD = AB = a
2
![]()
Khi đó ![]()
![]()
![]()
![]()
![]()
![]()
Lại có ![]()
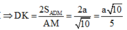
Từ đó ![]()
Chọn: C

Chọn đáp án D.
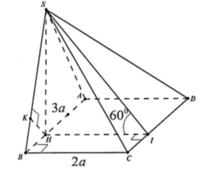
Ta có: ![]()
Kẻ 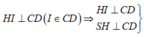
![]()
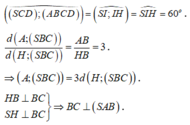
Kẻ ![]()
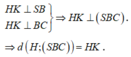
Xét tam giác SHI vuông tại H:
![]()
![]()
Xét tam giác SHB vuông tại B: 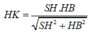
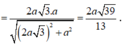
![]()
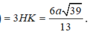

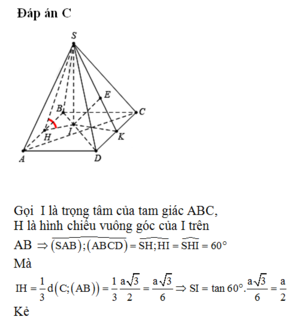
Chọn đáp án C
HC là hình chiếu của SC lên mặt phẳng (ABCD).
Góc giữa SC với mặt phẳng (ABCD) là: S C H ^ = 45 °
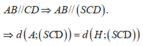
Kẻ 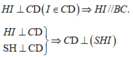
Kẻ 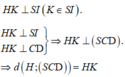
Ta có: ![]()
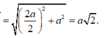
Tam giác SHC vuông cân tại H vì ![]()
Mặt khác: HI = AD = a
Xét tam giác SHI vuông tại H: 
![]()
![]()