Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(M\in\left(BMN\right);M\in SA\subset\left(SAC\right)\)
=>\(M\in\left(BMN\right)\cap\left(SAC\right)\)
\(C\in BN\subset\left(BMN\right);C\in\left(SAC\right)\)
=>\(C\in\left(BMN\right)\cap\left(SAC\right)\)
Do đó: \(CM=\left(BMN\right)\cap\left(SAC\right)\)
b: Xét (BMN) và (SAD) có
BN//AD
\(M\in\left(BMN\right)\cap\left(SAD\right)\)
Do đó: \(\left(BMN\right)\cap\left(SAD\right)=xy\); xy đi qua M và xy//BN//AD
d: Xét (MCD) và (SAB) có
CD//AB
\(M\in\left(MCD\right)\cap\left(SAB\right)\)
Do đó: (MCD) giao (SAB)=ab, ab đi qua M và ab//CD//AB

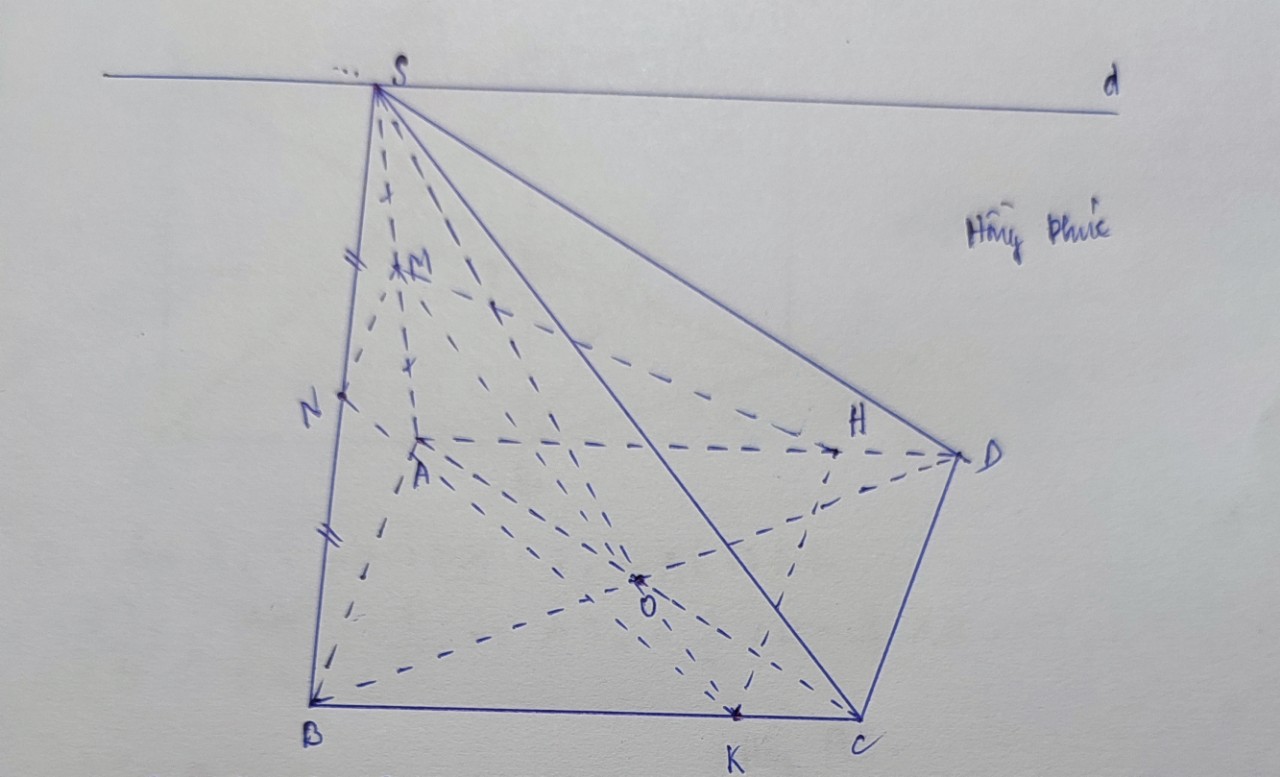
1: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
=>\(\left(SAC\right)\cap\left(SBD\right)=SO\)
AB//CD
S thuộc (SAB) giao (SCD)
=>(SAB) giao (SCD)=xy, xy qua S, xy//AB//DC
2:
Xét ΔSBC có SM/SB=SN/SC
nên MN//BC
=>MN//AD
=>AMND là hình thang
Xét ΔSBD có BM/BS=BO/BD
nên MO//SD
=>MO//(SAD)

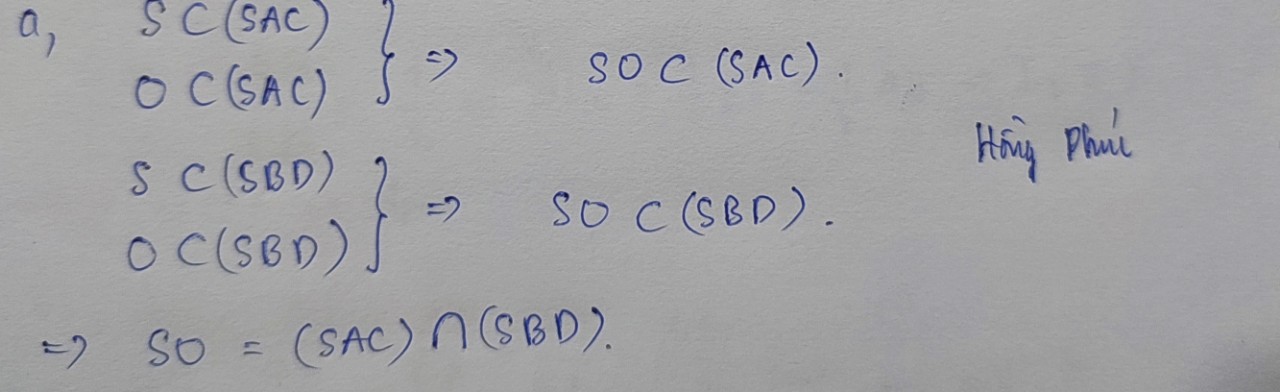
Mình chịu mình mới lớp 5