Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Giả sử S A → = x S A ' → ; S B → = y S B ' → ; S C → = z S C ' → .
Gọi G là trọng tâm tam giác ABC ⇒ G A → + G B → + G C → = 0 .
⇒ 3 G S → + S A → + S B → + S C → = 0
⇒ S G → = S A → 3 + S B → 3 + S C → 3 ⇒ S G → = x 3 . S A ' → + y 3 . S B ' → + z 3 . S C ' → 1
Do A ' B ' C ' đi qua G nên ba vectơ G A ' → ; G B ' → ; G C ' → đồng phẳng
Suy ra tồn tại 3 số i ; m ; n , i 2 + m 2 + n 2 ≠ 0 sao cho i . G A ' → + m . G B ' → + n . G C ' → = 0
i + m + n . G S → + i . S A ' → + m . S B ' → + n . S C ' → = 0
⇒ S G → = i i + m + n S A ' → + m i + m + n S B ' → + n i + m + n . S C ' → 2
Do S G ; S A ' ; S B ' ; S C ' không đồng phẳng nên từ (1) và (2) ta có
x 3 = i i + m + n ; y 3 = m i + m + n ; z 3 = n i + m + n
x + y + z 3 = i + m + n i + m + n = 1 ⇒ x + y + z = 3
Ta có 1 S A ' 2 + 1 S B ' 2 + 1 S C ' 2 = x 2 a 2 + y 2 b 2 + z 2 c 2
Áp dụng bất đẳng thức Bunyakovsky cho hai bộ số thực x a ; y b ; z c và a ; b ; c ta có .
x 2 a 2 + y 2 b 2 + z 2 c 2 a 2 + b 2 + c 2 ≥ x + y + z 2
⇔ 1 S A ' 2 + 1 S B ' 2 + 1 S C ' 2 ≥ x + y + z 2 a 2 + b 2 + c 2 = 3 a 2 + b 2 + c 2
Dấu “=” xảy ra khi x 2 a 2 = y 2 b 2 = z 2 c 2

Đáp án D.
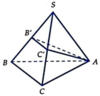
Gọi B',C' là trung điểm SB,SC ⇒ Thiết diện là Δ A B ' C '
Ta có S A ' B ' C ' = 1 2 A B ' 2 . A C ' 2 - A B ' → . A C ' → 2
A B ' → = 1 2 S B → - S A → ⇒ A B ' 2 = 1 4 S B 2 + S A 2 - S A → . S B → = a 2 4 5 - 4 cos α
Tương tự ta có A B ' → . A C ' → = a 2 4 4 - 3 cos α
Vậy S A B ' C ' = 1 2 a 4 16 5 - 4 cos α 2 - a 4 16 4 - 3 cos α 2 = a 2 8 7 cos 2 α - 16 cos α + 9

Chọn A
Xét một trường hợp đặc biệt của các điểm M, E, F ta tính được T = 1.

Phương pháp:
Sử dụng tỉ số diện tích, tỉ số thể tích để tính thể tích khối tứ diện MBSI thông qua thể tích khối tứ diện vuông SABC.
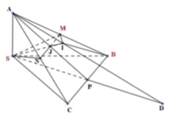

Áp dụng định lí Menelaus trong tam giác APD ta có:

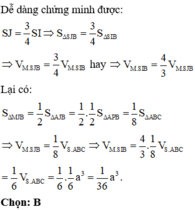
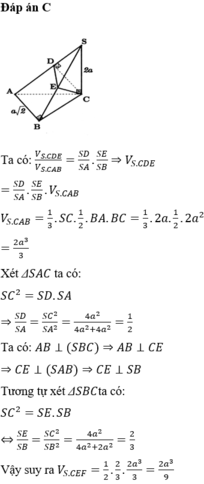

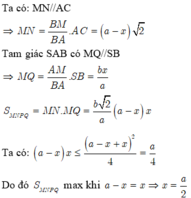
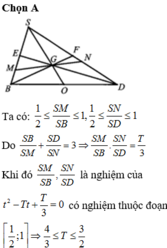

Chọn A