K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
24 tháng 12 2017
Chọn A
Cách giải:
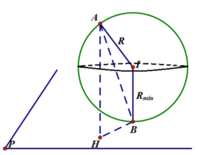
Gọi B là điểm tiếp xúc của mặt cầu (S) và mặt phẳng (P)
=> IB=R
Gọi H là hình chiếu của A xuống (P)

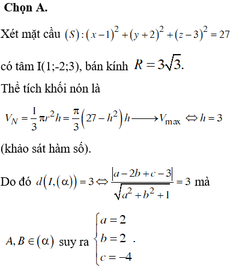


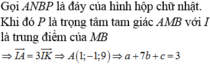
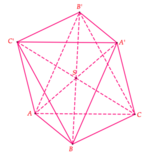
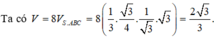
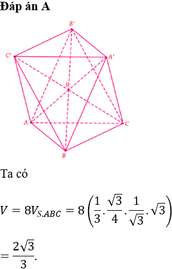


Đáp án A
Giả sử S A → = x S A ' → ; S B → = y S B ' → ; S C → = z S C ' → .
Gọi G là trọng tâm tam giác ABC ⇒ G A → + G B → + G C → = 0 .
⇒ 3 G S → + S A → + S B → + S C → = 0
⇒ S G → = S A → 3 + S B → 3 + S C → 3 ⇒ S G → = x 3 . S A ' → + y 3 . S B ' → + z 3 . S C ' → 1
Do A ' B ' C ' đi qua G nên ba vectơ G A ' → ; G B ' → ; G C ' → đồng phẳng
Suy ra tồn tại 3 số i ; m ; n , i 2 + m 2 + n 2 ≠ 0 sao cho i . G A ' → + m . G B ' → + n . G C ' → = 0
i + m + n . G S → + i . S A ' → + m . S B ' → + n . S C ' → = 0
⇒ S G → = i i + m + n S A ' → + m i + m + n S B ' → + n i + m + n . S C ' → 2
Do S G ; S A ' ; S B ' ; S C ' không đồng phẳng nên từ (1) và (2) ta có
x 3 = i i + m + n ; y 3 = m i + m + n ; z 3 = n i + m + n
x + y + z 3 = i + m + n i + m + n = 1 ⇒ x + y + z = 3
Ta có 1 S A ' 2 + 1 S B ' 2 + 1 S C ' 2 = x 2 a 2 + y 2 b 2 + z 2 c 2
Áp dụng bất đẳng thức Bunyakovsky cho hai bộ số thực x a ; y b ; z c và a ; b ; c ta có .
x 2 a 2 + y 2 b 2 + z 2 c 2 a 2 + b 2 + c 2 ≥ x + y + z 2
⇔ 1 S A ' 2 + 1 S B ' 2 + 1 S C ' 2 ≥ x + y + z 2 a 2 + b 2 + c 2 = 3 a 2 + b 2 + c 2
Dấu “=” xảy ra khi x 2 a 2 = y 2 b 2 = z 2 c 2