Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Giả sử S A → = x S A ' → ; S B → = y S B ' → ; S C → = z S C ' → .
Gọi G là trọng tâm tam giác ABC ⇒ G A → + G B → + G C → = 0 .
⇒ 3 G S → + S A → + S B → + S C → = 0
⇒ S G → = S A → 3 + S B → 3 + S C → 3 ⇒ S G → = x 3 . S A ' → + y 3 . S B ' → + z 3 . S C ' → 1
Do A ' B ' C ' đi qua G nên ba vectơ G A ' → ; G B ' → ; G C ' → đồng phẳng
Suy ra tồn tại 3 số i ; m ; n , i 2 + m 2 + n 2 ≠ 0 sao cho i . G A ' → + m . G B ' → + n . G C ' → = 0
i + m + n . G S → + i . S A ' → + m . S B ' → + n . S C ' → = 0
⇒ S G → = i i + m + n S A ' → + m i + m + n S B ' → + n i + m + n . S C ' → 2
Do S G ; S A ' ; S B ' ; S C ' không đồng phẳng nên từ (1) và (2) ta có
x 3 = i i + m + n ; y 3 = m i + m + n ; z 3 = n i + m + n
x + y + z 3 = i + m + n i + m + n = 1 ⇒ x + y + z = 3
Ta có 1 S A ' 2 + 1 S B ' 2 + 1 S C ' 2 = x 2 a 2 + y 2 b 2 + z 2 c 2
Áp dụng bất đẳng thức Bunyakovsky cho hai bộ số thực x a ; y b ; z c và a ; b ; c ta có .
x 2 a 2 + y 2 b 2 + z 2 c 2 a 2 + b 2 + c 2 ≥ x + y + z 2
⇔ 1 S A ' 2 + 1 S B ' 2 + 1 S C ' 2 ≥ x + y + z 2 a 2 + b 2 + c 2 = 3 a 2 + b 2 + c 2
Dấu “=” xảy ra khi x 2 a 2 = y 2 b 2 = z 2 c 2
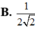
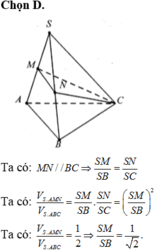

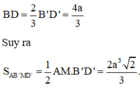
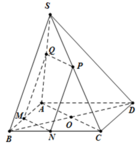
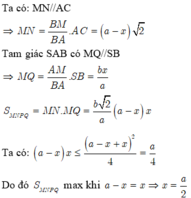

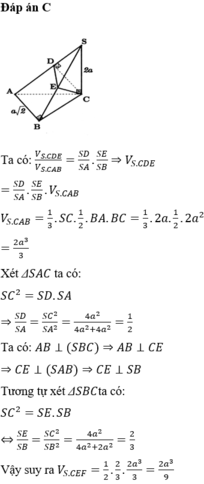
Đáp án D.
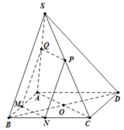
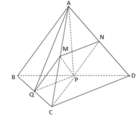
Gọi B',C' là trung điểm SB,SC ⇒ Thiết diện là Δ A B ' C '
Ta có S A ' B ' C ' = 1 2 A B ' 2 . A C ' 2 - A B ' → . A C ' → 2
A B ' → = 1 2 S B → - S A → ⇒ A B ' 2 = 1 4 S B 2 + S A 2 - S A → . S B → = a 2 4 5 - 4 cos α
Tương tự ta có A B ' → . A C ' → = a 2 4 4 - 3 cos α
Vậy S A B ' C ' = 1 2 a 4 16 5 - 4 cos α 2 - a 4 16 4 - 3 cos α 2 = a 2 8 7 cos 2 α - 16 cos α + 9