Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

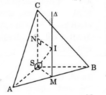
* Gọi M là trung điểm của tam giác SAB.
Tam giác SAB là tam giác vuông tại S có SM là đường trung tuyến nên ta có:
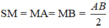
⇒ M là tâm đường tròn ngoại tiếp tam giác SAB.
* Kẻ Mt ⊥ (SAB), ta có: Mt// SC và Mt là trục đưởng tròn ngoại tiếp tam giác SAB.
Trong mp(Mt, SC), đường trung trực của SC cắt Mt tại điểm I.
Ta có: IS = IC. (1)
Và IS = IB = IA (2).
Từ (1) và (2) suy ra: IA = IB= IC = IS
Do đó, I là tâm mặt cầu ngoại tiếp hình chóp S.ABC
Bán kính mặt cầu ngoại tiếp hình chóp là :


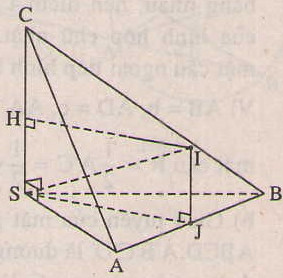
Gọi I là tâm cầu ngoại tiếp hình chóp tam giác S.ABC. Hạ IJ vuông góc (SAB), vì J cách đều 3 điểm S, A, B nên J cũng cách đều 3 điểm S, A, B.
Vì tam giác SAB vuông đỉnh S nên J là trung điểm của AB.
Ta có SJ = 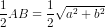 .
.
Do SC vuông góc (SAB) nên IJ // SC.
Gọi H là trung điểm SC, ta có SH = IJ =  .
.
Do vậy, IS2 = IJ2 + SJ2 = (a2 + b2 + c2)/4 và bán kính hình cầu ngoại tiếp S.ABC là
r = IS = 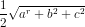 .
.
Diện tích mặt cầu là:
S = 4 πr2 = π(a2 + b2 + c2) (đvdt)
Thể tích khối cầu là :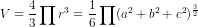
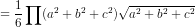 (đvtt)
(đvtt)

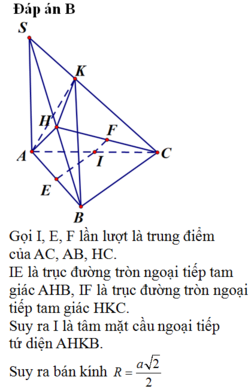
Đáp án B
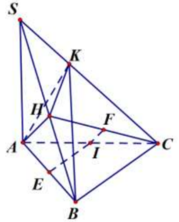
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC. IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
⇒ IA=IB=IC=IH=IK
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB.
Suy ra bán kính R= a 2 2

Đáp án B
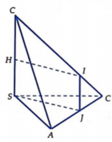
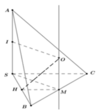
Gọi M,N lần lượt là trung điểm SC, AB
Vì ΔSAB vuông góc tại S nên N là tâm đường tròn ngoại tiếp ΔSAB .
Trong mặt phẳng (MSN) dựng hình chữ nhật MSNO thì ON là trục đường tròn ngoại tiếp ΔSAB và OM là đường trung trực của đoạn SC trong mặt phẳng (OSC)


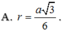




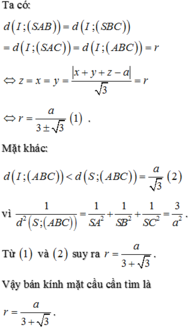
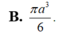
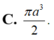
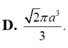


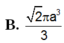







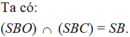
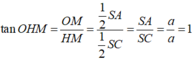
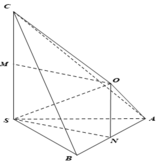
Bán kính mặt cầu ngoại tiếp hình chóp đã cho là R = \(\dfrac{1}{2}\sqrt{a^2+b^2+c^2}\).
Diện tích mặt cầu cần tìm là S = 4\(\pi\)R2 = (a2+b2+c2)\(\pi\).
Thể tích khối cầu cần tìm là V = 4/3.\(\pi\)R3 = \(\dfrac{\pi}{6}\sqrt{a^2+b^2+c^2}^3\).