Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

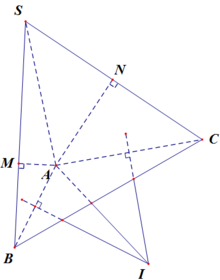
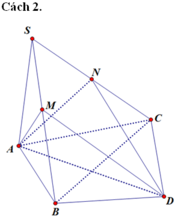
Mình không thạo vẽ hình trên này nên bạn tự vẽ hình nhé.
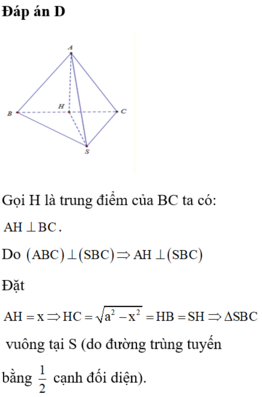
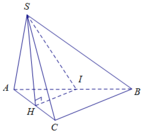
Gọi K là hình chiếu vuông góc của S trên BC.
Giả sử \(\overrightarrow{CK}=x\overrightarrow{CB}\left(0< x< 1\right)\)
Đặt \(SC=ka\Rightarrow\left\{{}\begin{matrix}BC=a\sqrt{k^2+4}\\AC=a\sqrt{k^2+8}\end{matrix}\right.\)
Ta có: \(\dfrac{1}{SK^2}=\dfrac{1}{SB^2}+\dfrac{1}{SC^2}=\dfrac{1}{\left(2a\right)^2}+\dfrac{1}{\left(ka\right)^2}\)
\(\Rightarrow SK=\dfrac{2ka}{\sqrt{k^2+4}}\)
Ta có:
\(\left(\left(SBC\right);\left(ABC\right)\right)=45^0\)
\(\Rightarrow\left(AB;SK\right)=45^0\)
\(\Leftrightarrow\dfrac{\overrightarrow{AB}.\overrightarrow{SK}}{AB.SK}=cos45^0\Leftrightarrow\dfrac{\overrightarrow{AB}.\overrightarrow{SK}}{AB.SK}=\dfrac{\sqrt{2}}{2}\)
Lại có:
\(\overrightarrow{AB}.\overrightarrow{SK}=\left(\overrightarrow{SB}-\overrightarrow{SA}\right).\left[x\overrightarrow{SB}+\left(1-x\right)\overrightarrow{SC}\right]\)
\(=xSB^2-x\overrightarrow{SA}.\overrightarrow{SB}+\left(x-1\right).\overrightarrow{SC}.\overrightarrow{SA}\)
\(=x.4a^2-x.4a^2.\dfrac{1}{2}+\left(x-1\right).\dfrac{4a^2+k^2a^2-a^2\left(k^2+8\right)}{2}\)
\(=2xa^2+\left(x-1\right).\left(-2a^2\right)=2a^2\)
\(\Rightarrow\dfrac{\sqrt{2}}{2}=\dfrac{2a^2}{2a.\dfrac{2ka}{\sqrt{k^2+4}}}\Leftrightarrow k=2\)
Do đó:
\(\left\{{}\begin{matrix}SC=2a\\BC=2a\sqrt{2}\\AC=2a\sqrt{3}\end{matrix}\right.\)
Ta có:
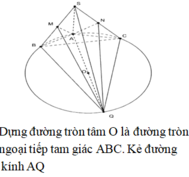
\(R=\sqrt{R_{SAB}^2+R_{ABC}^2-\dfrac{AB^2}{4}}\)
\(=\sqrt{\left(\dfrac{2a\sqrt{3}}{3}\right)^2+\left(a\sqrt{3}\right)^2-\dfrac{\left(2a\right)^2}{4}}=\dfrac{a\sqrt{30}}{3}\)
\(\Rightarrow S=4\pi R^2=4\pi.\dfrac{10}{3}a^2=\dfrac{40}{3}\pi a^2\)
dạ em nhờ các anh chị, các bạn giải giúp mình bài toán này với ạ!
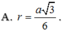
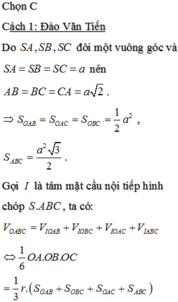



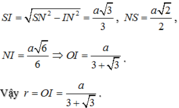

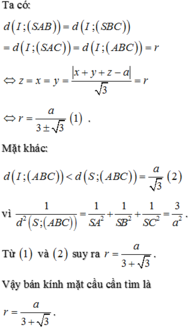

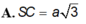
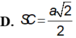



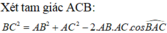



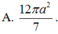
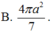
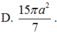


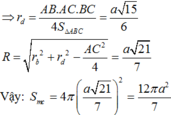
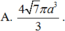
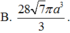
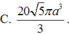
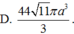



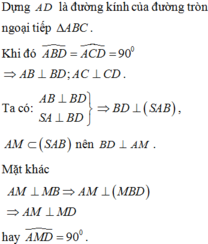


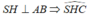
Chọn D.