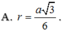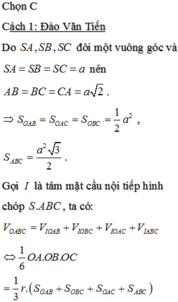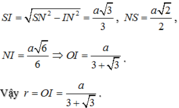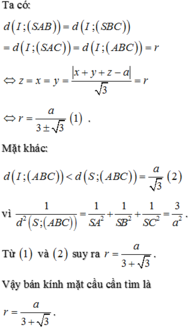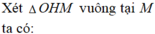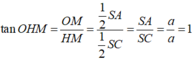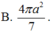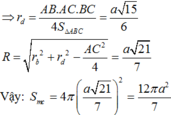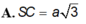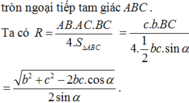Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A
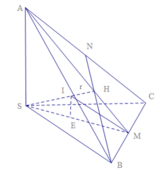
Cách 1. Áp dụng công thức: r = 3 V S t p (*) và tam giác đều cạnh x có diện tích S = x 2 3 4 .
Từ giả thiết S.ABC đều có SA=SB=SC. Lại có SA, SB, SC đôi một vuông góc và thể tích khối chóp S.ABC bằng a 3 6 nên ta có SA=SB=SC=a.
Suy ra AB=BC=CA=a 2 và tam giác ABC đều cạnh có độ dài a 2 . Do đó diện tích toàn phần của khối chóp S.ABC là
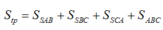
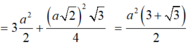
Thay vào (*) ta được:
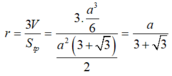

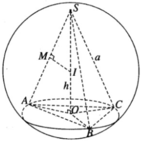
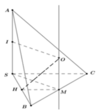
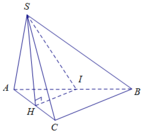
Giả sử ta có mặt cầu tâm I đi qua các đỉnh S, A, B, C của hình chóp. Mặt phẳng (ABC) cắt mặt cầu ngoại tiếp hình chóp theo giao tuyến là đường tròn tâm O ngoại tiếp tam giác ABC. Vì SA = SB = SC nên ta có SO ⊥ (ABC) và OS là trục của đường tròn tâm O. Do đó SO ⊥ AO. Trong tam giác SAO, đường trung trực của đoạn SA cắt SO tại I và ta được hai tam giác vuông đồng dạng là SIM và SAO, với M là trung điểm của cạnh SA.
Ta có 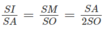
với SI = IA = IB = IC = r
Vậy 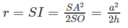
Do đó diện tích của mặt cầu ngoại tiếp hình chóp S.ABC đã cho là :
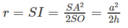

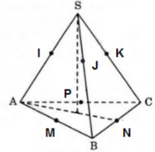
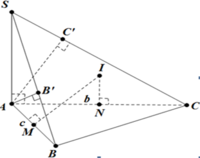
Gọi mặt cầu đã cho có tâm O và bán kính R.
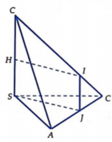
Gọi M, N, P lần lượt là trung điểm của AB, BC và CA.
Gọi I,J và K lần lượt là tiếp điểm của các cạnh bên SA, SB, SC với mặt cầu:
+ Từ giả thiết ta suy ra: OI ⊥ SA; OM ⊥ AB
Xét tam giác OIA và tam giác OMA có:
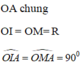
⇒ ∆ OIA = ∆OMA ( ch- cgv)
⇒ AM = AI.
Chứng minh tương tự có: BM= BJ và SI = SJ (1)
Mà AM = BM nên AI= BJ ; (2)
Từ (1) và (2) suy ra: SI+IA = SJ + BJ hay SA = SB (3)
* Chứng minh tương tự, ta có SB= SC (4).
Từ (3) và (4) suy ra: SA = SB = SC (*)
Mặt khác ; BM = BN (= BJ) và CN = CP (= CK)
Suy ra; AB = 2BM = BC = 2 CN = 2CP = CA
Do đó, tam giác ABC là tam giác đều (**)
Từ (*) và (**) suy ra, S. ABC là hình chóp tam giác đều.