
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Kẻ \(BK\perp AC\Rightarrow BK\perp\left(SAC\right)\)
\(\Rightarrow BK=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow BK=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Kẻ \(CP\perp BH\Rightarrow CP\perp\left(SBH\right)\)
\(\Rightarrow CP=d\left(C;\left(SBH\right)\right)\)
\(\widehat{CBP}=\widehat{ACB}=30^0\Rightarrow CH=BC.sin30^0=\dfrac{a\sqrt{3}}{2}\)
\(BH=\dfrac{AC}{2}=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)\(\Rightarrow SH=\sqrt{SB^2-BH^2}=a\)
Kẻ \(HE\perp BC\) , kẻ \(HF\perp SE\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)
\(HE=CH.sin30^0=\dfrac{a}{2}\)
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{5}}{5}\)

Đáp án D.
Đặt SH = x, tính SB, SC theo x. Sau đó áp dụng định lí cosin cho ∆ SBC
Tìm được ![]()

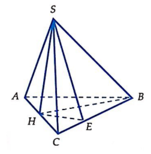
Gọi M là trung điểm AB là N là trung điểm BM
\(\Rightarrow CM\perp AB\) (trung tuyến đồng thời là đường cao trong tam giác đều)
NH là đường trung bình tam giác BCM \(\Rightarrow NH||CM\Rightarrow NH\perp AB\)
\(\Rightarrow AB\perp\left(SNH\right)\) \(\Rightarrow\left(SAB\right)\perp\left(SNH\right)\) với SN là giao tuyến
Trong mp (SNH), từ H kẻ \(HK\perp SN\Rightarrow HK\perp\left(SAB\right)\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)
\(CM=\dfrac{AC\sqrt{3}}{2}=6a\) ; \(NH=\dfrac{1}{2}CM=3a\)
\(\widehat{SNH}=60^0\Rightarrow HK=NH.sin60^0=\dfrac{3a\sqrt{3}}{2}\)