Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A

Gọi H là trung điểm của AC. Đỉnh S cách đều các điểm A, B, C
=> SH ⊥ (ABC)
Xác đinh được
![]()
Ta có MH // SA
![]()
Gọi I là trung điểm của AB => HI ⊥ AB
![]()
và chứng minh được HK ⊥ (SAB)
![]()
Trong tam giác vuông SHI tính được
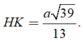

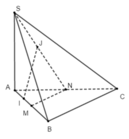
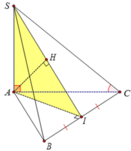
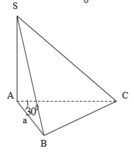
+ Ta có S A B ⊥ A B C S A C ⊥ A B C S A C ∩ S A B = S A ⇒ S A ⊥ A B C
+ Xác định điểm N, mặt phẳng qua SM và song song với BC cắt AC tại N ⇒ N là trung điểm của AC (MN//BC).
+ Xác định được góc giữa hai mặt phẳng (SBC) và (ABC) là S B A ^ = 60 °
⇒ SA = AB.tan 60 ° = 2a 3
AC = A B 2 + B C 2 = 2 a 2
+ Gọi IJ là đoạn vuông góc chung của AB và SN (điểm I thuộc AB và điểm J thuộc SN). Vậy khoảng cách giữa AB và SN là IJ. Ta sẽ biểu thị IJ → qua ba vectơ không cùng phương A B → ; A C → ; A S → .
I J → = I A → + A N → + N J → = m A B → + 1 2 A C → + p N S → = m A B → + 1 2 A C → + p N A → + A S → = m A B → + 1 − p 2 A C → + p A S →
Ta có: I J → ⊥ A B → I J → ⊥ N S → ⇔ I J → . A B → = 0 I J → . N S → = 0
Thay vào ta tính được m = -6/13; p = 1/13
Do đó: I J → = − 6 13 A B → + 6 13 A C → + 1 13 A S → . Suy ra
169 I J 2 = 36 A C 2 + 36 A B 2 + A S 2 − 72 A B → . A C → .
Thay số vào ta tính được IJ = 2 a 39 13 .
Vậy d(AB; SN) = 2 a 39 13 .
Đáp án D

Đáp án A
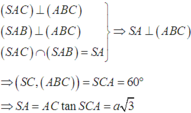
Gọi I,H lần lượt là hình chiếu vuông góc của A trên BC, SI, khi đó: d(A, (SBC)) =AH
Tam giác ABC đều cạnh a nên AI = a 3 2
Khi đó xét tam giác SAI :
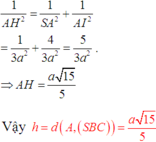

Đáp án B
Vì tam giác SAB cân tại S nên hạ SH ⊥ AB => H là trung điểm của AB.
Vì 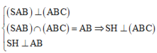
Tam giác SAB vuông cân tại S nên SA = SB = a 2
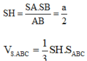
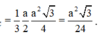
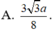
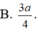
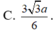
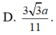
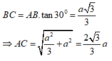
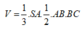
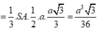
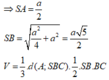
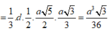
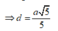
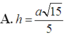
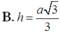
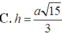
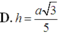
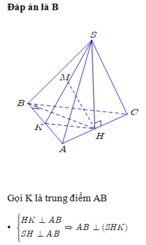
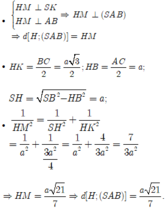
Chọn đáp án B
Gọi là H hình chiếu của đỉnh S xuống mặt phẳng (ABC). Khi đó, ta có
Ta có
Tương tự, ta cũng chứng minh được
Từ đó suy ra
Do SH ⊥ AB, BH ⊥ AB nên suy ra góc giữa (SAB) và (ABC) là góc SBH. Vậy SBH = 60 0
Trong tam giác vuông ABH, ta có
Trong tam giác vuông SHB, ta có