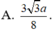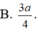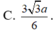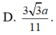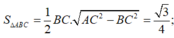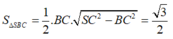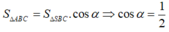Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
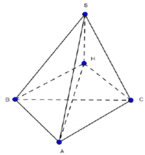
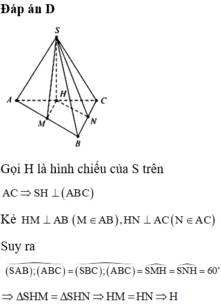
Gọi là H hình chiếu của đỉnh S xuống mặt phẳng (ABC). Khi đó, ta có
![]()
Ta có
![]()
Tương tự, ta cũng chứng minh được
![]()
Từ đó suy ra
![]()
Do SH ⊥ AB, BH ⊥ AB nên suy ra góc giữa (SAB) và (ABC) là góc SBH. Vậy SBH = 60 0
![]()
Trong tam giác vuông ABH, ta có
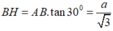
Trong tam giác vuông SHB, ta có
![]()
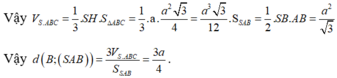

Do tam giác SAB đều và nằm trong mp vuông góc đáy \(\Rightarrow\) H là trung điểm AB
Gọi M là trung điểm AC\(\Rightarrow AM\perp AC\) (trung tuyến đồng thời là đường cao)
Gọi N là trung điểm AM \(\Rightarrow\) NH là đường trung bình tam giác AMH \(\Rightarrow NH||BM\Rightarrow NH\perp AC\)
\(\Rightarrow AC\perp\left(SNH\right)\)
Trong tam giác vuông SNH kẻ \(HK\perp SN\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(BM=\dfrac{a\sqrt{3}}{2}\Rightarrow NH=\dfrac{1}{2}BM=\dfrac{a\sqrt{3}}{4}\)
Hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{NH^2}=\dfrac{20}{3a^2}\Rightarrow NH=\dfrac{a\sqrt{15}}{10}\)