Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Góc giữa SA và AB là góc \(\widehat{SAB}\)
Do SABCD là chóp đều \(\Rightarrow SA=SB=SC=SD=2a\sqrt{6}\)
Áp dụng định lý hàm cosin trong tam giác SAB:
\(cos\widehat{SAB}=\dfrac{SA^2+AB^2-SB^2}{2SA.AB}=\dfrac{\sqrt{6}}{4}\)
\(\Rightarrow\widehat{SAB}\approx52^014'\)
b.
Góc giữa SB và BC là góc \(\widehat{SBC}\)
Do SABCD là chóp đều nên các góc đáy bằng nhau
\(\Rightarrow\widehat{SBC}=\widehat{SAB}=52^014'\)
c.
Do AD song song BC \(\Rightarrow\) góc giữa SC và AD bằng góc giữa SC và BC
\(\Rightarrow\) Góc giữa SC và AD bằng \(\widehat{SCB}\)
Mà chóp đều nên \(\widehat{SCB}=\widehat{SBC}=...\)
d.
Gọi O là tâm đáy
Do SABCD là chóp đều \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\)
Lại có \(AC\perp BD\) (2 đường chéo hình vuông)
\(\Rightarrow AC\perp\left(SBD\right)\)
\(\Rightarrow AC\perp SD\)
\(\Rightarrow\) Góc giữa SD và AC là 90 độ

\(\left\{{}\begin{matrix}SM\perp\left(MNPQ\right)\Rightarrow SM\perp PN\\PN\perp MN\end{matrix}\right.\) \(\Rightarrow PN\perp\left(SMN\right)\)
Lại có \(\left\{{}\begin{matrix}PN\perp\left(SMN\right)\\SN\in\left(SMN\right)\end{matrix}\right.\) \(\Rightarrow PN\perp SN\)

a: \(\widehat{SB;AB}=\widehat{SBA}\)
SA\(\perp\)(ABC)
=>\(SA\perp AB;SA\perp AC;SA\perp BC\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
=>\(\widehat{SBA}=60^0\)
=>\(\widehat{SB;AB}=60^0\)
b:
\(\widehat{SC;AC}=\widehat{SCA}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;AC}=60^0\)
c: ΔABC đều có AM là đường trung tuyến
nên \(AM=BC\cdot\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
Ta có: SA\(\perp\)(ABC)
AM\(\subset\)(ABC)
Do đó: SA\(\perp\)AM
=>ΔSAM vuông tại A
\(\widehat{SM;AM}=\widehat{SMA}\)
Xét ΔSMA vuông tại A có \(tanSMA=\dfrac{SA}{AM}=\dfrac{a\sqrt{3}}{\dfrac{a\sqrt{3}}{2}}=2\)
=>\(\widehat{SMA}\simeq63^026'\)
=>\(\widehat{SM;AM}\simeq63^026'\)
a.
Góc giữa SB và AB là góc \(\widehat{SBA}\)
Trong tam giác vuông SAB:
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\Rightarrow\widehat{SBA}=60^0\)
b.
Góc giữa SC và AC là góc \(\widehat{SCA}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
c.
Góc giữa SM và AM là góc \(\widehat{SMA}\)
AM là trung tuyến tam giác đều \(\Rightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow tan\widehat{SMA}=\dfrac{AM}{SA}=2\Rightarrow\widehat{SMA}=60^026'\)

Chọn D
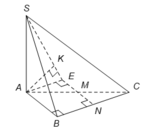
Xác định được
![]()
![]()
Gọi N là trung điểm BC, suy ra MN//AB.
Lấy điểm E đối xứng với N qua M, suy ra ABNE là hình chữ nhật.
Do đó
![]()
![]()
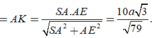

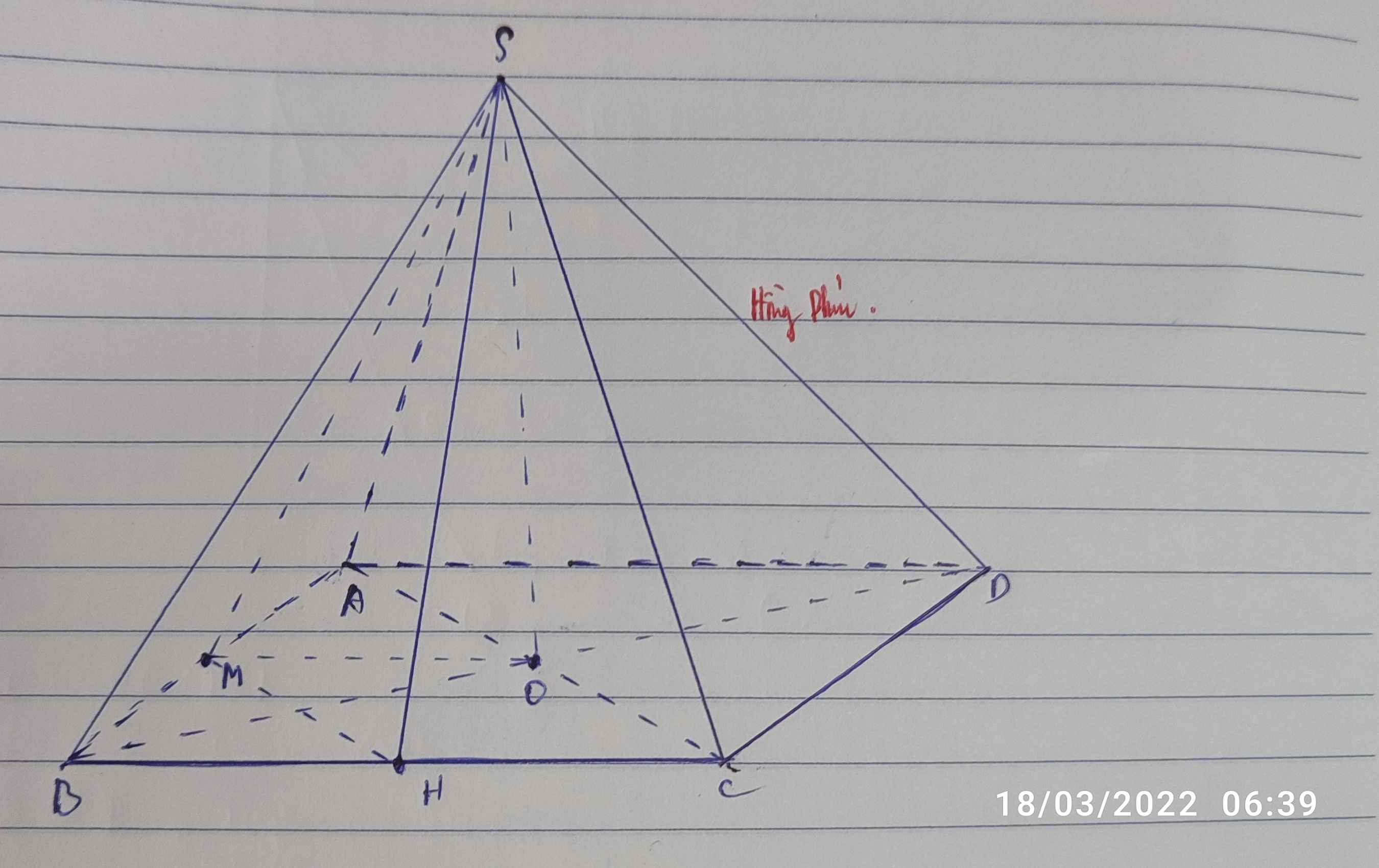

a.
Góc giữa SM và MQ là góc SMQ
Do chóp đều nên \(SM=SN=SP=SQ=8a\sqrt{2}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{SMQ}=\dfrac{SM^2+MQ^2-SQ^2}{2SM.MQ}=\dfrac{\sqrt{2}}{4}\)
\(\Rightarrow\widehat{SMQ}\approx69^018'\)
b.
Góc giữa SN và NP là góc SNP
Do chóp đều \(\Rightarrow\widehat{SNP}=\widehat{SMQ}=69^018'\)
c.
Do MN song song PQ nên góc giữa SQ và MN bằng góc giữa SQ và PQ là góc SQP
Do chóp đều nên \(\widehat{SQP}=\widehat{SMQ}=69^018'\)
d.
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(MNPQ\right)\)
\(\Rightarrow SO\perp NQ\)
Mà \(NQ\perp MP\) (2 đường chéo hình vuông)
\(\Rightarrow NQ\perp\left(SMP\right)\Rightarrow NQ\perp SP\)
\(\Rightarrow\) Góc giữa SP và NQ bằng 90 độ