Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Gọi K là trung điểm của BC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔCAB có
O,K lần lượt là trung điểm của CA,CB
=>OK là đường trung bình
=>OK//AB và \(OK=\dfrac{AB}{2}\)
=>\(\overrightarrow{OK}=\dfrac{\overrightarrow{AB}}{2}\)
=>\(\overrightarrow{AB}=2\cdot\overrightarrow{OK}\)
Xét ΔOBC có OK là đường trung tuyến
nên \(\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{OK}\)
=>\(\overrightarrow{AB}=\overrightarrow{OB}+\overrightarrow{OC}\)
=>M trùng với B
Bài 2:
Xét ΔABC có
M,P lần lượt là trung điểm của AB,AC
=>MP là đường trung bình của ΔABC
=>MP//BC và MP=BC/2
=>MP=CN
mà MP//NC
nên MPCN là hình bình hành
=>\(\overrightarrow{MP}=\overrightarrow{NC}\)
=>\(\overrightarrow{MP}=-\overrightarrow{CN}\)
=>\(\overrightarrow{MP}+\overrightarrow{CN}=\overrightarrow{0}\)
mà \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\)
nên K trùng với P

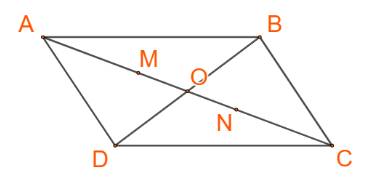
a) Áp dụng tính chất trọng tâm ta có: \(\overrightarrow {MA} + \overrightarrow {MD} + \overrightarrow {MB} = \overrightarrow 0 \)
Suy ra M là trọng tâm của tam giác ADB
Vậy M nằm trên đoạn thẳng AO sao cho \(AM = \frac{2}{3}AO\)
b) Tiếp tục áp dụng tính chất trọng tâm \(\overrightarrow {ND} + \overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \)
Suy ra N là trọng tâm của tam giác BCD
Vậy N nằm trên đoạn thẳng OD sao cho \(ON = \frac{1}{3}OD\)
c) Áp dụng tính chất trung điểm ta có: \(\overrightarrow {PM} + \overrightarrow {PN} = \overrightarrow 0 \)
Suy ra P là trung điểm của đoạn thẳng MN
Vậy điểm P trùng với điểm O.

Gọi O là tâm bình hành
\(\overrightarrow{MA}+2\overrightarrow{MB}+2\overrightarrow{MC}+\overrightarrow{MD}=\overrightarrow{0}\Leftrightarrow6\overrightarrow{MO}+\overrightarrow{OA}+2\overrightarrow{OB}+2\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}\)
Dễ dàng nhìn ra trong hình bình hành ABCD tâm O thì: \(\hept{\begin{cases}\overrightarrow{OA}+\overrightarrow{OD}=-\frac{1}{2}\overrightarrow{AB}\\\overrightarrow{OB}+\overrightarrow{OD}=\frac{1}{2}\overrightarrow{AB}\end{cases}}\)--->thế lên trên:
\(\Rightarrow6\overrightarrow{MO}-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AB}=\overrightarrow{0}\Leftrightarrow\overrightarrow{OM}=\frac{1}{12}\overrightarrow{AB}\)---> Dễ dàng có được M là điểm cố định (Vì các điểm O,A,B đều cố định)
Vậy điểm M được xác định bằng cách lấy đường thẳng qua O song song AB rồi trong nửa mặt phẳng bờ là BD có chứa điểm C ta lấy điểm M thuộc đường thẳng vừa dựng được sao cho đoạn OM có độ dài đúng bằng 1/12 độ dài AB.
Gọi O là giao điểm hai đoạn thẳng AC và BD.
Dựng điểm M như sau:
Trên nửa mặt phẳng bờ AC phía B, vẽ tia Ot song song AB.
Trên tia này, Bạn lấy điểm M cách O một đoạn bằng MỘT PHẦN SÁU AB.
Đó là điểm cần tìm.
 |
 |

Gọi P và Q lần lượt là trung điểm AB và CD \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MP}\\\overrightarrow{MC}+\overrightarrow{MD}=2\overrightarrow{MQ}\end{matrix}\right.\)
\(\left|\overrightarrow{MA}-\overrightarrow{BM}\right|=\left|\overrightarrow{MC}-\overrightarrow{DM}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MC}+\overrightarrow{MD}\right|\)
\(\Leftrightarrow\left|2\overrightarrow{MP}\right|=\left|2\overrightarrow{MQ}\right|\)
\(\Leftrightarrow MP=MQ\)
Tập hợp M là đường trung trực của đoạn PQ

Do \(\overrightarrow{NP}=\overrightarrow{DC}\); \(\overrightarrow{AM}=\overrightarrow{BA}\Rightarrow\overrightarrow{MA}=\overrightarrow{AB}\).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
Vì vậy \(\overrightarrow{NP}=\overrightarrow{MA}\) nên tứ giác NPAM là hình bình hành.
Vì vậy \(\overrightarrow{PA}=\overrightarrow{NM}\). (1)
Mà \(\overrightarrow{MN}=\overrightarrow{DA}\) suy ra \(\overrightarrow{NM}=\overrightarrow{AD}\) . (2)
Mặt khác \(\overrightarrow{AD}=\overrightarrow{BC}\) (do tứ giác ABCD là hình bình hành). (3)
Từ (1);(2);(3) suy ra:\(\overrightarrow{PA}=\overrightarrow{BC}\).
Mà \(\overrightarrow{PQ}=\overrightarrow{BC}\Rightarrow\overrightarrow{PQ}=\overrightarrow{PA}\).
Vì vậy hai điểm A và Q trùng nhau nên \(\overrightarrow{AQ}=\overrightarrow{0}\).