Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1:
Gọi O là giao điểm của AC và BD.

Ta có:
\(\begin{array}{l}\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {BG} = \overrightarrow a + \overrightarrow {BG} ;\\\overrightarrow {CG} = \overrightarrow {CB} + \overrightarrow {BG} = \overrightarrow {DA} + \overrightarrow {BG} = - \overrightarrow b + \overrightarrow {BG} ;\end{array}\)(*)
Lại có: \(\overrightarrow {BD} =\overrightarrow {BA} + \overrightarrow {AD} = - \overrightarrow a + \overrightarrow b \).
\(\overrightarrow {BG} ,\overrightarrow {BD} \) cùng phương và \(\left| {\overrightarrow {BG} } \right| = \frac{2}{3}BO = \frac{1}{3}\left| {\overrightarrow {BD} } \right|\)
\( \Rightarrow \overrightarrow {BG} = \frac{1}{3}\overrightarrow {BD} = \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right)\)
Do đó (*) \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AG} = \overrightarrow a + \overrightarrow {BG} = \overrightarrow a + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\\\overrightarrow {CG} = -\overrightarrow b + \overrightarrow {BG} = -\overrightarrow b + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b ;\end{array} \right.\)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .\)
Cách 2:
Gọi AE, CF là các trung tuyến trong tam giác ABC.
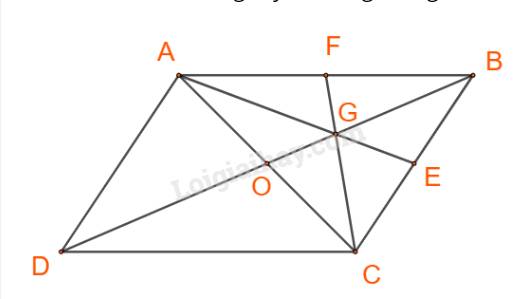
Ta có:
\(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AE} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\overrightarrow {AB} + \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)} \right] \\= \frac{1}{3}\left( {2\overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {CG} = \frac{2}{3}\overrightarrow {CF} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\left( {\overrightarrow {CB} + \overrightarrow {CD} } \right) + \overrightarrow {CB} } \right] = \frac{1}{3}\left( {2\overrightarrow {CB} + \overrightarrow {CD} } \right) = \frac{1}{3}\left( { - 2\overrightarrow {AD} - \overrightarrow {AB} } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b \)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .\)

Do EF là đường trung bình tam giác ABC \(\Rightarrow I\) là trung điểm AD
\(\overrightarrow{AI}=\frac{1}{2}\overrightarrow{AD}=\frac{1}{2}\overrightarrow{u}\)
\(\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}=\frac{2}{3}\overrightarrow{u}\)
\(\overrightarrow{DE}=\frac{1}{2}\overrightarrow{BA}=-\frac{1}{2}\overrightarrow{AB}=-\overrightarrow{AF}=-\overrightarrow{v}\)
\(\overrightarrow{DC}=\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{AB}+\overrightarrow{AD}=-2\overrightarrow{AF}+\overrightarrow{AD}=\overrightarrow{u}-2\overrightarrow{v}\)

a) Giả sử \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{BO}+\overrightarrow{OA}\right)+\left(\overrightarrow{DO}+\overrightarrow{OC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\) (đúng do tứ giác ABCD là hình bình hành).
b) \(\overrightarrow{ME}+\overrightarrow{FN}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{FC}+\overrightarrow{CN}\)
\(=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\).
Do các tứ giác AMOE, MOFB, OFCN, EOND cũng là các hình bình hành.
Vì vậy \(\overrightarrow{CN}=\overrightarrow{FO}=\overrightarrow{BM};\overrightarrow{FC}=\overrightarrow{ON}=\overrightarrow{ED}\).
Do đó: \(\overrightarrow{ME}+\overrightarrow{FN}=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\)
\(=\left(\overrightarrow{MA}+\overrightarrow{BM}\right)+\left(\overrightarrow{AE}+\overrightarrow{ED}\right)\)
\(=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}\) (Đpcm).

Bài 1:
Gọi K là trung điểm của BC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔCAB có
O,K lần lượt là trung điểm của CA,CB
=>OK là đường trung bình
=>OK//AB và \(OK=\dfrac{AB}{2}\)
=>\(\overrightarrow{OK}=\dfrac{\overrightarrow{AB}}{2}\)
=>\(\overrightarrow{AB}=2\cdot\overrightarrow{OK}\)
Xét ΔOBC có OK là đường trung tuyến
nên \(\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{OK}\)
=>\(\overrightarrow{AB}=\overrightarrow{OB}+\overrightarrow{OC}\)
=>M trùng với B
Bài 2:
Xét ΔABC có
M,P lần lượt là trung điểm của AB,AC
=>MP là đường trung bình của ΔABC
=>MP//BC và MP=BC/2
=>MP=CN
mà MP//NC
nên MPCN là hình bình hành
=>\(\overrightarrow{MP}=\overrightarrow{NC}\)
=>\(\overrightarrow{MP}=-\overrightarrow{CN}\)
=>\(\overrightarrow{MP}+\overrightarrow{CN}=\overrightarrow{0}\)
mà \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\)
nên K trùng với P

\(a,\) \(\overrightarrow{IA}=2\overrightarrow{IB}-4\overrightarrow{IC}\)
\(\overrightarrow{IA}=2\overrightarrow{IB}-2\overrightarrow{IC}-2\overrightarrow{IC}=2\overrightarrow{CB}-2\overrightarrow{IC}\)
\(=2\left(\overrightarrow{AB}-\overrightarrow{AC}\right)-2\left(\overrightarrow{AC}-\overrightarrow{AI}\right)\)
\(\overrightarrow{IA}=2\overrightarrow{AB}-2\overrightarrow{AC}-2\overrightarrow{AC}+2\overrightarrow{AI}\)
\(\overrightarrow{IA}=\dfrac{2}{3}\overrightarrow{AB}-\dfrac{4}{3}\overrightarrow{AC}\)
\(b,\overrightarrow{IJ}=\overrightarrow{AJ}-\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{IA}=\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AB}-\dfrac{4}{3}\overrightarrow{AC}=\dfrac{4}{3}\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\left(1\right)\)
\(\overrightarrow{JG}=\overrightarrow{AG}-\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{AM}-\dfrac{2}{3}\overrightarrow{AB}\)\((\) \(\) \(M\) \(trung\) \(điểm\) \(BC)\)
\(\overrightarrow{JG}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}-\dfrac{2}{3}\overrightarrow{AB}=-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=-\dfrac{1}{3}\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\overrightarrow{IJ}=-4\overrightarrow{JG}\Rightarrow I,J,G\) \(thẳng\) \(hàng\)

Từ M kẻ đường thẳng song song với AB, cắt AD tại E.
Khi đó tứ giác ABME là hình bình hành.
Do đó: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AE} \).
Dễ thấy: \(AE = BM = \frac{1}{2}BC = \frac{1}{2}AD\)
\( \Rightarrow \overrightarrow {AE} = \frac{1}{2}\overrightarrow {AD} \)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \)
Vậy \(\overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \)
Chú ý khi giải
+) Dựng hình hình hành sao cho đường chéo là vecto cần biểu thị, 2 cạnh của nó song song với giá của hai vecto đang biểu thị theo.