Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: D = m − 1 3 m = m 2 + 3 ; D x = 2 − 1 5 m = 2 m + 5 ; D y = m 2 3 5 = 5 m − 6
Vì m 2 + 3 ≠ 0 , ∀ m nên hệ phương trình luôn có nghiệm duy nhất x = D x D = 2 m + 5 m 2 + 3 y = D y D = 5 m − 6 m 2 + 3
Theo giả thiết, ta có:
x + y < 1 ⇔ 2 m + 5 m 2 + 3 + 5 m − 6 m 2 + 3 < 1 ⇔ 7 m − 1 m 2 + 3 < 1
⇔ 7 m − 1 < m 2 + 3 ⇔ m 2 − 7 m + 4 > 0 ⇔ m > 7 + 33 2 m < 7 − 33 2
Đáp án cần chọn là: A

\(\hept{\begin{cases}mx+y=m^2+m+1\\-x+my=m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(my-m^2\right)+y-m^2-m-1=0\\x=my-m^2\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}\left(m^2y-m^2\right)+\left(y-1\right)-\left(m^3+m\right)=0\\x=my-m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(m^2+1\right)\left(y-m-1\right)=0\\x=my-m^2\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}y=m+1\\x=m\left(m+1\right)-m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=m\\y=m+1\end{cases}}\)
\(\Rightarrow\)\(x^2+y^2=2m^2+2m+1=2\left(m+\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}\)
Dấu "=" xảy ra khi \(m=\frac{-1}{2}\) hay hệ có nghiệm \(\left(x;y\right)=\left(\frac{-1}{2};\frac{1}{2}\right)\)

\(\left\{{}\begin{matrix}x+y=m\\2x+my=2m+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+2y=2m\\2x+my=2m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2-m\right)y=-2\\x+y=m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{m-2}\\x=\dfrac{m^2-2m-2}{m-2}\end{matrix}\right.\)
Vậy ..


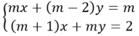
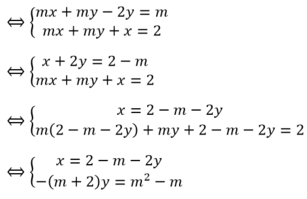

Đáp án: D
Để hệ phương trình có nghiệm thì phương trình (1) có nghiệm, tức là:
Vậy giá trị lớn nhất của m để hệ phương trình có nghiệm là 6.