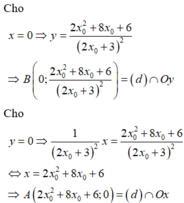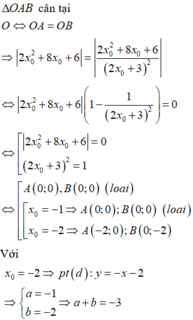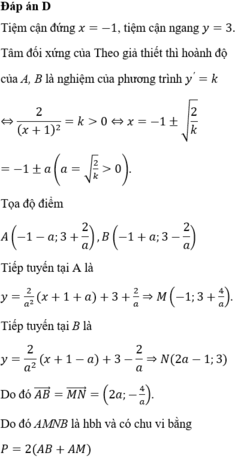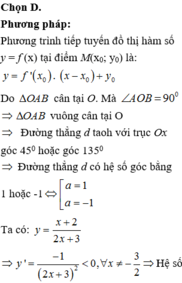Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi M a ; a 3 − 3 a suy ra PTTT tại M là: y = 3 a 2 − 3 x − a + a 3 − 3 a d
Ta có:
d ∩ Ox = B − a 3 + 3 a 3 a 2 − 3 + a ; 0
Phương trình hoành độ giao điểm của d và C là :
x 3 − 3 x = 3 a 2 − 3 x − a + a 3 − 3 a
⇔ x − a x 2 + ax + a 2 − 3 x − a = 3 a 2 − 3 x − a ⇔ x − a x 2 + a x − 2 a 2 = 0 ⇔ x − a 2 x + 2 a = 0 ⇔ x = − 2 a ⇒ A − 2 a ; − 8 a 3 + 6 a
Do A, M, B luôn thuộc tiếp tuyến d nên để M là trung điểm của AB thì:
2 y M = y A + y B
⇔ 2 a 3 − 6 a = − 8 a 3 + 6 a ⇔ 10 a 3 = 12 a ⇔ a = 0 a = ± 6 5
Do M ≠ 0 ⇒ a ≠ 0 ⇒ a = ± 6 5 .
Vậy có 2 điểm M thỏa mãn yêu cầu.

Đáp án D
Phương pháp:
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x o .
+) Tìm giao điểm của tiếp tuyến với các trục tọa độ.
+) Tính OA, OB, giải phương trình tìm x o → Phương trình tiếp tuyến và kết luận.