Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Để y = (m - 1)x + 2m - 3 là hàm số bậc nhất thì a \(\ne\) 0 \(\Leftrightarrow\) m - 1 \(\ne\) 0 \(\Leftrightarrow\) m \(\ne\) 1
y = (m - 1)x + 2m - 3 đồng biến trên R \(\Leftrightarrow\) a > 0 \(\Leftrightarrow\) m - 1 > 0 \(\Leftrightarrow\) m > 1
y = (m - 1)x + 2m - 3 nghịch biến trên R \(\Leftrightarrow\) a < 0 \(\Leftrightarrow\) m - 1 < 0 \(\Leftrightarrow\) m < 1
b, f(1) = 2
\(\Leftrightarrow\) (m - 1).1 + 2m - 3 = 2
\(\Leftrightarrow\) m - 1 + 2m - 3 = 2
\(\Leftrightarrow\) m = 2
Với m = 2 ta có:
f(2) = (2 - 1).2 + 2.2 - 3 = 3
Vậy f(2) = 3
c, f(-3) = 0
\(\Leftrightarrow\) (m - 1).0 + 2m - 3 = 0
\(\Leftrightarrow\) 2m = 3
\(\Leftrightarrow\) m = 1,5
Vì m > 1 (1,5 > 1)
\(\Rightarrow\) m - 1 > 0
hay a > 0
Vậy hàm số y = f(x) = (m - 1).x + 2m - 3 đồng biến trên R
Chúc bn học tốt!

Lời giải:
a. Vì $\sqrt{3}-1>0$ nên hàm trên là hàm đồng biến trên $\mathbb{R}$
b.
$F(0)=(\sqrt{3}-1).0+1=1$
$F(\sqrt{3}+1)=(\sqrt{3}-1)(\sqrt{3}+1)+1=(3-1)+1=3$

Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)

Lời giải:
a. Ta thấy: $(\sqrt{3}-1)(3-1)=2(\sqrt{3}-1)>0$ nên hàm số trên là hàm đồng biến trên $\mathbb{R}$
b.
$F(0)=2(\sqrt{3}-1).0+1=1$
$F(\sqrt{3}+1)=2(\sqrt{3}-1)(\sqrt{3}+1)+1=2(3-1)+1=5$
$F[(\sqrt{3}+1)(3+1)]=F[4(\sqrt{3}+1)]=2(\sqrt{3}-1).4(\sqrt{3}+1)+1$
$=8(3-1)+1=17$

a: f(x)=3x^2
a=3>0
=>Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: f(1)=f(-1)=3*1^2=3
f(2)=3*2^2=12
f(-4)=3*(-4)^2=48
c: f(x)=48
=>x^2=48/3=16
=>x=4 hoặc x=-4
d; 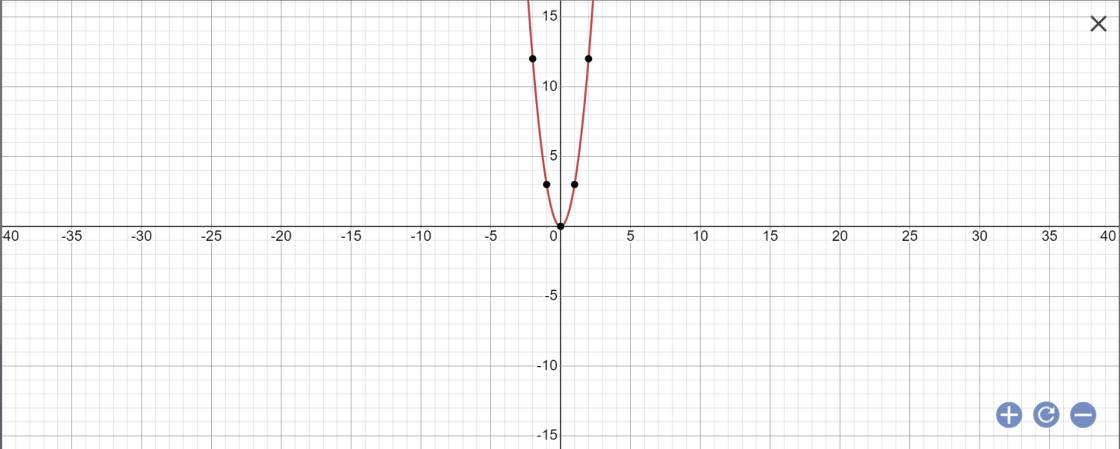

a: Hàm số này đồng biến vì \(2-\sqrt{3}>0\)
b: \(f\left(2+\sqrt{3}\right)=4-3-1=0\)
\(f\left(\sqrt{3}\right)=2\sqrt{3}-3-1=2\sqrt{3}-4\)
Ấn vào đây tham khảo nhé!