Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có - 1 30 = ∫ 1 2 x - 1 f ( x ) d x = 1 2 ∫ 1 2 f ( x ) d x - 1 2
= 1 2 x - 1 2 f ( x ) 1 2 - 1 2 ∫ 1 2 x - 1 2 f ' x d x
⇔ ∫ 1 2 x - 1 2 f ' ( x ) d x = 1 15
Ta lại có ∫ 1 2 x - 1 4 d x = 1 5 x - 1 5 1 2 = 1 5
Từ giả thiết và các kết quả ta có
9 ∫ 1 2 f ' ( x ) 2 d x - 6 ∫ 1 2 x - 1 2 f ' ( x ) d x + ∫ 1 2 x - 1 4 d x = 0
Mặt khác:
9 ∫ 1 2 f ' ( x ) 2 d x - 6 ∫ 1 2 x - 1 2 f ' ( x ) d x + ∫ 1 2 x - 1 4 d x = ∫ 1 2 3 f ' ( x ) - x - 1 2 2
Do vậy xét trên đoạn [1;2] , ta có
3 f ' ( x ) - ( x - 1 ) 2 = 0 ⇔ f ' ( x ) = 1 3 x - 1 2 ⇒ f ( x ) = 1 9 x - 1 3 + c
Lại do f(2) = 0 nên C + 1 9 = 0 ⇔ C = - 1 9 ⇒ f ( x ) = 1 9 x - 1 3 - 1 9
Suy ra I = 1 9 ∫ 1 2 x - 1 3 - 1 d x = 1 36 x - 1 4 1 2 - 1 9 x - 1 1 2 = - 1 12

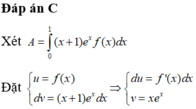
⇒ A = x e x f x 1 0 - ∫ 0 1 x e x f ' x d x = - ∫ 0 1 x e x f ' x d x = 1 - e 2 4
Xét ∫ 0 1 x 2 e 2 x d x = e 2 x 1 2 x 2 - 1 2 x + 1 4 1 0 = e 2 - 1 4
Ta có ∫ 0 1 f ' x 2 d x + 2 ∫ 0 1 x e x f ' x d x + ∫ 0 1 x 2 e 2 x f x d x = 0 ⇔ ∫ 0 1 f ' x + x . e x 2 d x = 0 f ' x + x . e x = 0 , ∀ x ∈ 0 ; 1 d o f ' x + x . e x 2 ≥ 0 , ∀ x ∈ 0 ; 1 ⇒ f ' x = - x e x ⇒ f x = 1 - x e x + C f 1 = 0 ⇒ f x = 1 - x e x ⇒ I = ∫ 0 1 f x d x = ∫ 0 1 1 - x e x d x = 2 - x e x 1 0 = e - 2

Đáp án C
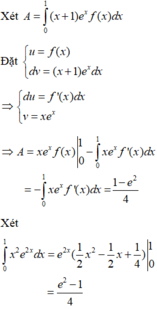
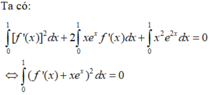
⇒ f ' ( x ) + x e x = 0 , ∀ x ∈ [ 0 ; 1 ] ( d o f ' x + x e x 2 ≥ 0 , ∀ x ∈ [ 0 ; 1 ] ) ⇒ f ' ( x ) = − x e x ⇒ f ( x ) = ( 1 − x ) e x + C f ( 1 ) = 0 ⇒ f ( x ) = ( 1 − x ) e x ⇒ I = ∫ 0 1 f ( x ) d x = ∫ 0 1 ( 1 − x ) e x d x = ( 2 − x ) e x 1 0 = e − 2

Đáp án A
Phương pháp : Sử dụng phương pháp đổi biến, đặt x = a – t.
Cách giải : Đặt x = a – t => dx = –dt. Đổi cận 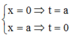
=> 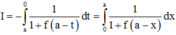
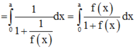
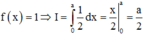
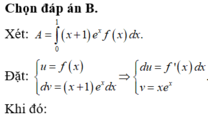
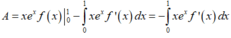
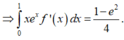
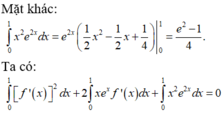
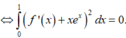
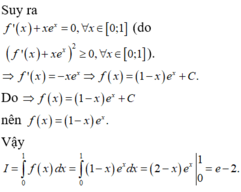
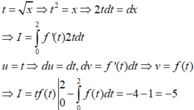
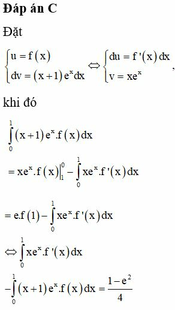
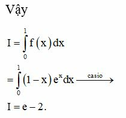
Đáp án là A