Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử M( x o ; y o ) ∈ (C). Gọi d 1 là khoảng cách từ M đến tiệm cận đứng và d 2 là khoảng cách từ M đến tiệm cận ngang, ta có:
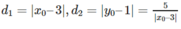
Có hai điểm thỏa mãn đầu bài, đó là hai điểm có hoành độ x o = 3 + 5 hoặc x o = 3 - 5

a) Học sinh tự làm.
b) Tiệm cận đứng là đường thẳng x = 3.
Tiệm cận ngang là đường thẳng y = 1.
Do đó, giao điểm của hai đường tiệm cận là I(3; 1). Thực hiện phép biến đổi:
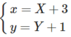
Ta được
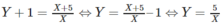
Vì Y = 5/X là hàm số lẻ nên đồ thị (C) của hàm số này có tâm đối xứng là gốc tọa độ I của hệ tọa độ IXY.
c) Giả sử M(x0; y0) ∈ (C). Gọi d1 là khoảng cách từ M đến tiệm cận đứng và d2 là khoảng cách từ M đến tiệm cận ngang, ta có:
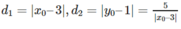
Có hai điểm thỏa mãn đầu bài, đó là hai điểm có hoành độ x0 = 3 + 5 hoặc x0 = 3 - 5

b) Tiệm cận đứng là đường thẳng \(x=3\)
Tiệm cận ngang là đường thẳng \(y=1\)


Hàm nhận \(x=3\) là tiệm cận đứng và \(y=1\) là tiệm cận ngang
Gọi \(M\left(a;b\right)\Rightarrow b=\dfrac{a+2}{a-3}\)
Khoảng cách đến tiệm cận đứng: \(\left|x_M-3\right|=\left|a-3\right|\)
Khoảng cách đến tiệm cận ngang: \(\left|y_M-1\right|=\left|b-1\right|\)
Ta có hệ: \(\left\{{}\begin{matrix}b=\dfrac{a+2}{a-3}\\\left|b-1\right|=5\left|a-3\right|\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(4;6\right)\\M\left(2;-4\right)\end{matrix}\right.\) có 2 điểm

Đồ thị hàm nhận \(x=1\) là tiệm cận đứng
Gọi \(M\left(a;b\right)\Rightarrow b=\dfrac{2a+1}{a-1}\)
Khoảng cách từ M đến trục hoành: \(\left|y_M\right|=\left|b\right|\)
Khoảng cách từ M đến tiệm cận đứng: \(\left|x_M-1\right|=\left|a-1\right|\)
Ta được hệ: \(\left\{{}\begin{matrix}b=\dfrac{2a+1}{a-1}\\\left|b\right|=\left|a-1\right|\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(0;-1\right);\left(4;3\right)\)
Có 2 điểm M thỏa mãn: \(\left[{}\begin{matrix}M\left(0;-1\right)\\M\left(4;3\right)\end{matrix}\right.\)

Đáp án A
Gọi
 với
a
≢
1
.
với
a
≢
1
.
Tiệm cận đứng của (C) là x-1.
Ta có 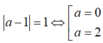 . Vậy
. Vậy ![]() .
.
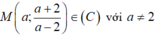
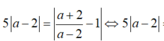
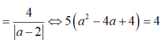
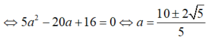
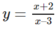

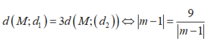
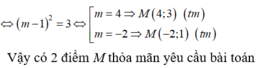
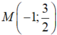
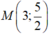

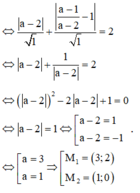
Xét \(M\left(m;1+\frac{5}{m-3}\right)\) thuộc đồ thị đã cho
Theo yêu cầu bài tài <=> \(\left|m-3\right|=\left|\frac{5}{m-3}\right|\Leftrightarrow m=3\pm\sqrt{5}\)
Vậy \(M\left(3\pm\sqrt{5};1\pm\sqrt{5}\right)\)