Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=4x^3-4mx\Rightarrow y'\left(1\right)=4-4m\)
\(A\left(1;1-m\right)\)
Phương trình tiếp tuyến d tại A có dạng:
\(y=\left(4-4m\right)\left(x-1\right)+1-m\)
\(\Leftrightarrow\left(4-4m\right)x-y+3m-3=0\)
\(d\left(B;d\right)=\dfrac{\left|\dfrac{3}{4}\left(4-4m\right)-1+3m-3\right|}{\sqrt{\left(4-4m\right)^2+1}}=\dfrac{1}{\sqrt{\left(4-4m\right)^2+1}}\le1\)
Dấu "=" xảy ra khi và chỉ khi \(4-4m=0\Rightarrow m=1\)
y′=4x3−4mx⇒y′(1)=4−4my′=4x3−4mx⇒y′(1)=4−4m
A(1;1−m)A(1;1−m)
Phương trình tiếp tuyến d tại A có dạng:
y=(4−4m)(x−1)+1−my=(4−4m)(x−1)+1−m
⇔(4−4m)x−y+3m−3=0⇔(4−4m)x−y+3m−3=0
d(B;d)=∣∣∣34(4−4m)−1+3m−3∣∣∣√(4−4m)2+1=1√(4−4m)2+1≤1d(B;d)=|34(4−4m)−1+3m−3|(4−4m)2+1=1(4−4m)2+1≤1
Dấu "=" xảy ra khi và chỉ khi 4−4m=0⇒m=1

x^2+(y-1)^2=4
=>R=2 và I(0;1)
A(1;1-m) thuộc (C)
y'=4x^3-4mx
=>y'(1)=4-4m
PT Δsẽ là y=(4-m)(x-1)+1-m
Δ luôn đi qua F(3/4;0) và điểm F nằm trong (λ)
Giả sử (Δ) cắt (λ) tại M,N
\(MN=2\sqrt{R^2-d^2\left(I;\Delta\right)}=2\sqrt{4-d^2\left(I;\Delta\right)}\)
MN min khi d(I;(Δ)) max
=>d(I;(Δ))=IF
=>Δ vuông góc IF
Khi đó, Δ có 1 vecto chỉ phương là: vecto u vuông góc với vecto IF=(3/4;p-1)
=>vecto u=(1;4-4m)
=>1*3/4-(4-4m)=0
=>m=13/16

Hàm bậc 2 có \(a=1>0;-\dfrac{b}{2a}=-\dfrac{m+1}{2}\) nên đồng biến trên \(\left(-\dfrac{m+1}{2};+\infty\right)\)
Để hàm đồng biến trên khoảng đã cho thì \(-\dfrac{m+1}{2}\le-2\Rightarrow m\ge3\)
\(\Rightarrow\) Tập đã cho có vô số phần tử
Còn phần tử nguyên thì có \(2021-3=2018\) phần tử

Chọn A.
Ta có: y’ = 3x2 – 4x + 2.
Tiếp tuyến tại M, N của (C) vuông góc với đường thẳng y = -x + 2017. Nên tiếp tuyến tại M và N có hệ số góc là 1
Hoành độ x1, x2 của các điểm M, N là nghiệm của phương trình 3x2 – 4x + 2 = 1.
Suy ra x1 + x2 = 4/3 ( hệ thức Vi-et).

\(y'=\dfrac{-1}{\left(x-1\right)^2}\)
Gọi phương trình đường thẳng d qua A có dạng: \(y=k\left(x-a\right)+1\)
d tiếp xúc (C) khi và chỉ khi hệ sau có nghiệm:
\(\left\{{}\begin{matrix}\dfrac{-x+2}{x-1}=k\left(x-a\right)+1\\\dfrac{-1}{\left(x-1\right)^2}=k\end{matrix}\right.\)
\(\Rightarrow\dfrac{-x+2}{x-1}=\dfrac{-\left(x-a\right)}{\left(x-1\right)^2}+1\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)=x-a-\left(x-1\right)^2\)
\(\Leftrightarrow2x^2-6x+3=-a\) (1)
Để có đúng 1 tiếp tuyến qua A khi (1) có đúng 1 nghiệm
\(\Rightarrow y=-a\) tiếp xúc \(y=2x^2-6x+3\)
\(\Leftrightarrow-a=-\dfrac{3}{2}\Rightarrow a=\dfrac{3}{2}\)






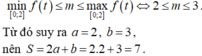
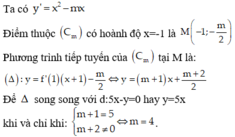
Tiếp tuyến có hệ số góc bằng 1
\(y'=\dfrac{m\left(3m+1\right)-\left(-m^2+m\right)}{\left(x+m\right)^2}=\dfrac{4m^2}{\left(x+m\right)^2}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\dfrac{4m^2}{\left(x+m\right)^2}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}2m=x+m\\-2m=x+m\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}x=m\\x=-3m\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=\dfrac{m^2-m}{3m+1}\\-3m=\dfrac{m^2-m}{3m+1}\end{matrix}\right.\)
\(\Leftrightarrow...\)