Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^3-3\left(m+1\right)x^2+2mx+m+2=0\left(1\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-3mx-2x-m-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^2-x\left(3m+2\right)-m-2\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2-x\left(3m+2\right)-m-2=0\left(2\right)\end{matrix}\right.\)
\(\left(1\right)có\) \(3ngo\) \(phân\) \(biệt\Leftrightarrow\left(2\right)\) \(có\) \(2\) \(ngo\) \(phân\) \(biệt\ne1\)
\(\Leftrightarrow\left\{{}\begin{matrix}g\left(1\right)\ne0\\\Delta>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{-3}{4}\\\left(3m+2\right)^2-4\left(-m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{-3}{4}\\9m^2+16m+12>0\left(luôn-đúng\right)\end{matrix}\right.\)
\(\Rightarrow m\ne\dfrac{-3}{4}\) \(thì\left(1\right)\) \(có\) \(3ngo\) \(phân\) \(biệt\)
\(do\left(2\right)\) \(\) \(có\) \(2\) \(ngo\) \(phân\) \(biệt\ne1\Rightarrow x3=1\)
\(\Rightarrow x1+x2=2\)
\(vi-ét\Rightarrow\left\{{}\begin{matrix}x1+x2=3m+2\\x1x2=-m-2\end{matrix}\right.\)
\(\Rightarrow3m+2=2\Leftrightarrow m=0\left(tm\right)\)

\(y=\dfrac{1}{3}\left(m-1\right)x^3-\left(m-1\right)x^2+\left(m+3\right)x-2\)
\(y'=\)\(x^2\left(m-1\right)-2x\left(m-1\right)+m+3\)
a)\(y'=0\)\(\Leftrightarrow x^2\left(m-1\right)-2x\left(m-1\right)+m+3=0\)
Xét m=1 => pt tt: 3=0 (vô lí)
=> \(m\ne1\)
Để y'=0 có hai nghiệm pb cùng dấu
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\x_1x_2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-16m+16>0\\\dfrac{m+3}{m-1}>0\end{matrix}\right.\)\(\Rightarrow m< -3\)
b)y'=0 có hai nghiệm \(\Leftrightarrow\Delta\ge0\) \(\Leftrightarrow m\le-3\)
Theo viet có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m-1}=2\\x_1x_2=\dfrac{m+3}{m-1}\end{matrix}\right.\)
Có x12+x22=4
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\)\(4-\dfrac{2\left(m+3\right)}{m-1}=4\)
\(\Leftrightarrow m=-3\) (tm)
Vậy m=-3
(đúng không ạ?)

Chọn B
Vì ba nghiêm phân biệt x 1 , x 2 , x 3 lập thành một cấp số cộng nên ta đặt : x 1 = x 0 + d , x 2 = x 0 , x 3 = x 0 + d ( d ≠ 0 )
Theo giả thuyết Ta có: x3+3x2 – (24+m)x – 26- n= (x – x1)(x-x2)(x-x3)
=(x-xo+d)(x-xo)(x-xo-d)= x3 – 3xox2+ (3xo2-d2)x-xo3+ xod2 với mọi x

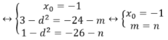
Vậy với m=n thì ba nghiệm phân biệt của phương trình lập thành một cấp số cộng

\(f'\left(x\right)=\dfrac{\left(2x-3\right)\left(x-1\right)-x^2+3x-7}{\left(x-1\right)^2}=\dfrac{x^2-2x-4}{\left(x-1\right)^2}\)
\(f'\left(x\right)=0\Leftrightarrow x^2-2x-4=0\Rightarrow\left[{}\begin{matrix}x=1+\sqrt{5}\\x=1-\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow x_1^2+x_2^2=12\)
Hoặc bạn dùng Vi-ét cũng được, tùy

1a.
\(y'=3x^2.f'\left(x^3\right)-2x.g'\left(x^2\right)\)
b.
\(y'=\dfrac{3f^2\left(x\right).f'\left(x\right)+3g^2\left(x\right).g'\left(x\right)}{2\sqrt{f^3\left(x\right)+g^3\left(x\right)}}\)
2.
\(f'\left(x\right)=\left(m-1\right)x^3+\left(m-2\right)x^2-2mx+3=0\)
Để ý rằng tổng hệ số của vế trái bằng 1 nên pt luôn có nghiệm \(x=1\), sử dụng lược đồ Hooc-ne ta phân tích được:
\(\Leftrightarrow\left(x-1\right)\left[\left(m-1\right)x^2+\left(2m-3\right)x-3\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(m-1\right)x^2+\left(2m-3\right)x-3=0\left(1\right)\end{matrix}\right.\)
Xét (1), với \(m=1\Rightarrow x=-3\)
- Với \(m\ne1\Rightarrow\Delta=\left(2m-3\right)^2+12\left(m-1\right)=4m^2-3\)
Nếu \(\left|m\right|< \dfrac{\sqrt{3}}{2}\Rightarrow\) (1) vô nghiệm \(\Rightarrow f'\left(x\right)=0\) có đúng 1 nghiệm
Nếu \(\left|m\right|>\dfrac{\sqrt{3}}{2}\Rightarrow\left(1\right)\) có 2 nghiệm \(\Rightarrow f'\left(x\right)=0\) có 3 nghiệm

\(f'\left(x\right)=2cos2x-4\left(1-2m\right)sin2x-2m\)
Phương trình \(f'\left(x\right)=0\) có nghiệm
\(\Leftrightarrow2cos2x-4\left(1-2m\right)sin2x=2m\) có nghiệm
\(\Leftrightarrow cos2x-2\left(1-2m\right)sin2x=m\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(1^2+4\left(1-2m\right)^2\ge m^2\)
\(\Leftrightarrow15m^2-16m+5\ge0\)
\(\Leftrightarrow15\left(m-\dfrac{8}{15}\right)^2+\dfrac{11}{15}\ge0\) (luôn đúng)
Vậy \(f'\left(x\right)=0\) có nghiệm với mọi m